Комбинации тел | ЕГЭ по математике (профильной)

Комбинации тел | ЕГЭ по математике (профильной) ЕГЭ
На чтение 6 мин. Просмотров 29 Опубликовано

. Комбинации тел | Подготовка к ЕГЭ по математике

Задача 4. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 5. Объем параллелепипеда равен 5. Найдите высоту цилиндра.

Решение:   показать

Задача 5. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 18. Найдите объем параллелепипеда.

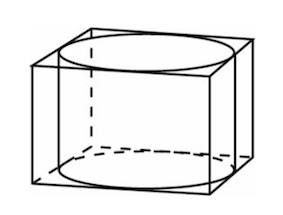Комбинации тел | ЕГЭ по математике (профильной)Решение:   показать

Задача 6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

Решение:  показать

Высота призмы равна высоте цилиндра.

В основании правильной призмы – квадрат.

Диаметр основания цилиндра – это сторона основания призмы (сторона квадрата).

Площадь боковой поверхности S_{bok} призмы есть сумма площадей 4-х равных прямоугольников. Измерения таких прямоугольников – это 1 призмы есть сумма площадей 4-х равных прямоугольников. Измерения таких прямоугольников – это 1  и 2.

Поэтому

 S_{bok}=4cdot1cdot2=8.

Ответ: 8.

Задача 7. В основании прямой призмы лежит квадрат со стороной 8. Боковые ребра равны frac{5}{pi}.. Боковые ребра равны frac{5}{pi}. Найдите объем цилиндра, описанного около этой призмы.

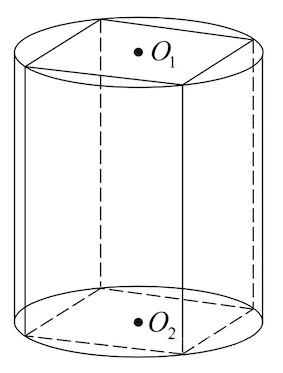
Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

Диагональ квадрата – диаметр (D) основания цилиндра:

D=2R=sqrt{8^2 8^2}=8sqrt2;

R=4sqrt2.

Тогда

V=pi R^2cdot H=pi (4sqrt2)^2cdot frac{5}{pi}=160.

Ответ: 160.

Задача 8. Около шара описан цилиндр, площадь поверхности которого равна 81. Найдите площадь поверхности шара.

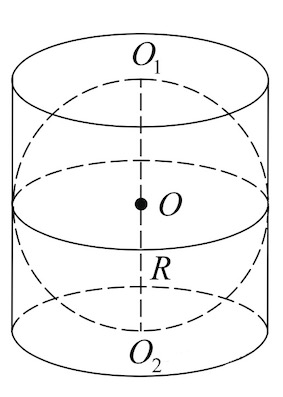
Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

Так как площадь поверхности цилиндра с радиусом основания R и высотой  H и высотой  H есть

S=2pi R^2 2pi RH, то

81=2pi R^2 2pi RH.

Но при этом высота цилиндра H – это диаметр шара, то есть 2R=H. – это диаметр шара, то есть 2R=H.

Поэтому

81=2pi R^2 4pi R^2;

81=6pi R^2.

Откуда

pi R^2=frac{81}{6}.

Площадь же поверхности шара вычисляется по формуле

S=4pi R^2.

Поэтому

S=4cdot frac{81}{6}=54.

Ответ: 54.

Задача 9.  Цилиндр описан около шара. Объем цилиндра равен 6. Найдите объем шара.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

Объем цилиндра с радиусом основания R и высотой H и высотой H есть

V_{silindr}=pi R^2H.

По условию V_{silidr}=6, поэтому

6=pi R^2H.

При этом H=2R, стало быть

6=pi cdot R^2cdot 2R=2pi R^3.

Объем же шара вычисляется по формуле

V_{shar}=frac{4pi R^3}{3}.

Значит

V_{shar}=frac{2cdot 6}{3}=4.

Ответ: 4.

Задача 10. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 156. Найдите объем конуса.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

Комбинации тел | ЕГЭ по математике (профильной)

Объем шара есть

V_{shar}=frac{4pi R^3}{3}.

По условию объем шара равен 156, поэтому

156=frac{4pi R^3}{3},

откуда

frac{pi R^3}{3}=39.

Объем же конуса с  радиусом основания R и высотой H=R и высотой H=R есть

Про ЕГЭ:  18.01.2022 История 11 класс новые тренировочные варианты ЕГЭ 2022 с ответами | ЕГЭ ОГЭ СТАТГРАД ВПР 100 баллов

V_{konus}=frac{pi R^2H}{3}=frac{pi R^3}{3}=39.

Ответ: 39.

Задача 11. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 27. Найдите объем шара.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

V_{konus}=frac{pi R^2H}{3}.

Согласно условию

27=frac{pi R^2H}{3}.

Тогда

V_{shar}=frac{4pi R^3}{3}=4cdot V_{konus}=4cdot 27=108.

Ответ: 108.

Задача 12. Середина ребра куба со стороной 0,8 является центром шара радиуса 0,4. является центром шара радиуса 0,4. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите frac{S}{pi}. части поверхности шара, лежащей внутри куба. В ответе запишите frac{S}{pi}.

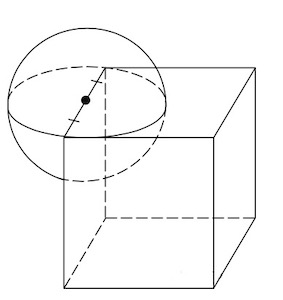
Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

S=frac{S_{shar}}{4}=frac{4pi R^2}{4}=pi R^2=0,16pi.

frac{S}{pi}=0,16.

Ответ: 0,16.

Задача 13. Вершина A куба ABCDA_1B_1C_1D_1 куба ABCDA_1B_1C_1D_1  со стороной 0,7 является центром сферы, проходящей через точку A_1 является центром сферы, проходящей через точку A_1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину frac{S}{pi} части сферы, содержащейся внутри куба. В ответе запишите величину frac{S}{pi}.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

Куб плоскостями граней  (ABCD,; AA_1B_1B,;AA_1D_1D) отсекает от сферы frac{1}{8}) отсекает от сферы frac{1}{8}  часть. Значит и площадь поверхности части сферы, содержащейся внутри куба, будет frac{1}{8} от площади поверхности сферы. А поскольку радиус сферы – есть ребро куба, то

S=frac{1}{8}cdot 4pi R^2=frac{pi cdot 0,7^2}{2}=0,245pi.

Наконец,

frac{S}{pi}=0,245.

Ответ: 0,245.

Задача 14. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 45.

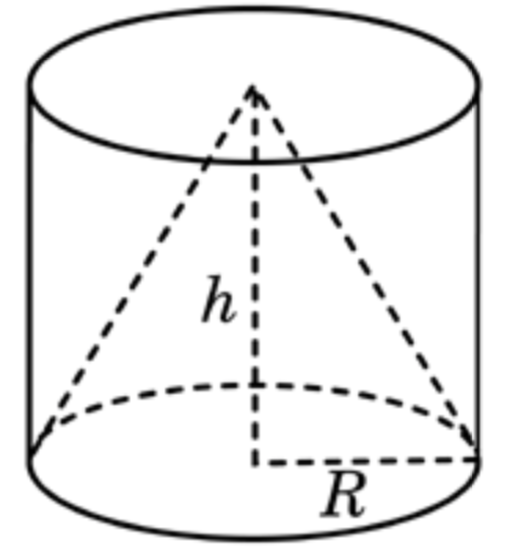
Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 15. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 44sqrt2. Найдите площадь боковой поверхности конуса.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 16. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 5. и высотой 5. Найдите его объем, деленный на pi.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 17. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 18. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 156. Найдите объем конуса.

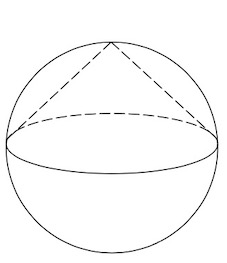
Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 19. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен 5sqrt2.  Найдите образующую конуса.

Про ЕГЭ:  Под ред. Ященко И.В. ЕГЭ 2017. Математика. Базовый уровень. 30 тренировочных вариантов экзаменационных работ | Подготовка к ОГЭ, ГИА и ЕГЭ. Математика. | Глубинная психология: учения и методики

Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 20. В основании прямой призмы лежит прямоугольный треугольник с катетами 1 и 10. и 10. Боковые ребра равны frac{6}{pi}. Найдите объем цилиндра, описанного около этой призмы.

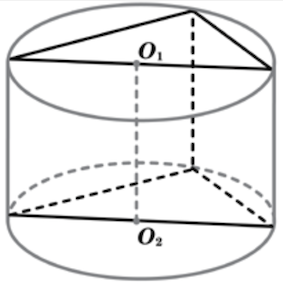
Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 21. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен sqrt3, а высота равна 1. а высота равна 1.

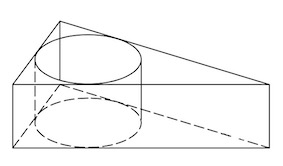
Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 22.  Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2sqrt3, а высота равна 4. а высота равна 4.

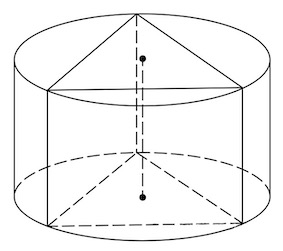
Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 23. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 27.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:   показать

Задача 24. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен  sqrt3, а высота равна 1., а высота равна 1.

Решение:  показать

Высота призмы равна высоте цилиндра.

В основании правильной пирамиды – равносторонний треугольник.

Радиус вписанного в него круга (основания цилиндра) ищем из прямоугольного треугольника с углом 30°(помечен на рисунке красным цветом, – в нем катет, прилежащий к углу 30°(помечен на рисунке красным цветом, – в нем катет, прилежащий к углу 30°, есть половина стороны треугольника):

tg30^{circ}=frac{r}{frac{a}{2}},

где  a – cсторона треугольника.

frac{sqrt3}{3}=frac{sqrt3}{frac{a}{2}};

a=6.

Площадь боковой поверхности правильной треугольной призмы – есть сумма площадей  трех равных прямоугольников с измерениями 6 и 1 и 1 (высота призмы).

S_{bok}=3cdot 6cdot 1=18.

Ответ: 18.

Задача 25. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен sqrt{0,03} , а высота равна 1. , а высота равна 1.

Решение:  показать

Боковая поверхность правильной шестиугольной призмы составлена из шести равных друг другу прямоугольников с измерениями a (сторона основания) и h (сторона основания) и h (высота призмы).

Выразим a через заданный  r через заданный  r:

Правильный шестиугольник составлен из шести равных правильных треугольников (см. рис.).

Высота (радиус вписанной окружности) OH является и биссектрисой, и медианой.

Из треугольника AOH:

a^2=(frac{a}{2})^2 r^2;

a^2=frac{a^2}{4} r^2;

4a^2=a^2 4r^2;

a^2=frac{4r^2}{3};

a=frac{2sqrt3r}{3}.

Подставляя известное значение r, имеем:

a=frac{2sqrt3cdot sqrt{0,03}}{3}=0,2.

Тогда

S_{bok}=6cdot 0,2cdot 1=1,2.

Ответ: 1,2.

Про ЕГЭ:  ЕГЭ. Теория по кодификатору. Россия

Задача 26. Около куба с ребром sqrt{243}  описан шар. Найдите объем этого шара, деленный на pi.  описан шар. Найдите объем этого шара, деленный на pi.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

Диаметр шара (2R) есть диагональ куба (на рис. – BD_1) есть диагональ куба (на рис. – BD_1, например).

Если ребро куба равно sqrt{243}, то диагональ есть

sqrt{(sqrt{243})^2 (sqrt{243})^2 (sqrt{243})^2}

(дважды применили т. Пифагора, к каждому из треугольников, выделенных цветом на рис.).

Комбинации тел | ЕГЭ по математике (профильной)

Итак, диагональ куба (диаметр шара) равна sqrt{729}=27. Поэтому радиус шара равен frac{27}{2}.. Поэтому радиус шара равен frac{27}{2}.

Итак, объем шара  таков:

V=frac{4cdot pi cdot R^3}{3}=frac{4cdot pi cdot (frac{27}{2})^3}{3}=frac{6561pi}{2}=3280,5pi .

Наконец,

frac{V}{pi}=3280,5.

Ответ: 3280,5.

Задача 27. Куб вписан в шар радиуса 6,5sqrt3. Найдите объем куба.

Комбинации тел | ЕГЭ по математике (профильной)

Решение:  показать

Диаметр шара (2R) – есть диагональ куба (например, BD_1) – есть диагональ куба (например, BD_1).

Пусть a – ребро куба. Тогда

BD_1=sqrt{a^2 a^2 a^2}=asqrt3.

C учетом условия 2R=13sqrt3,  имеем:

13sqrt=asqrt3;

a=13.

Итак,

V=a^3=13^3=2197.

Ответ: 2197.

тестВы можете пройти тест “Комбинация тел”

Автор: |

Нет комментариев

Печать страницы

Теорема пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2 ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

  1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
  2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
  3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$$30$$45$$60$
$sinα$${1}/{2}$${√2}/{2}$${√3}/{2}$
$cosα$${√3}/{2}$${√2}/{2}$${1}/{2}$
$tgα$${√3}/{3}$$1$$√3$
$ctgα$$√3$$1$${√3}/{3}$
05 Стереометрия
Оцените статью
ЕГЭ Live
© 2024 ЕГЭ Live