Производные основных элементарных функций
Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Поэтому приведем стандартную таблицу производных.
Функция f (x) | Производная f’ (х) |
|---|---|
С (т. е. константа, любое число) | 0 |
х | 1 |
xn | nxn-1 |
√x | 1/(2√x) |
sin x | cos x |
cos x | -sin x |
tg x | 1/cos2(х) |
ctg x | -1/sin2x |
ex | ex |
ax | ax * ln a |
ln x | 1/x |
logax | 1/(x * ln a) |
Элементарные функции можно складывать, умножать друг на друга, находить их разность или частное — словом, выполнять любые математические операции. Но для этого существуют определенные правила.
Что такое производная и зачем она нужна
Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:
Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю. |
Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:
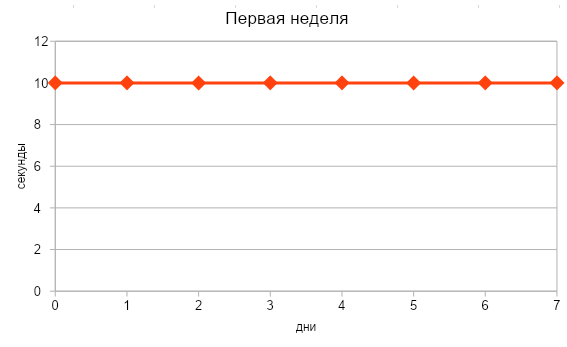
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.
у = 10
у′ = 0
Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.
у = 10 3х
Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1, а также по правилам вычисления производных (c*f(x))’=cf'(x) и (f(x) g(x))’=f'(x) g'(x).
у = 10 3х
у′ = 0 3
у′ = 3
Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.
Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.
Быстрее освоить производные поможет
обучение на курсах по математике в онлайн-школе Skysmart.
Общие правила дифференцирования
Для решения задач на дифференцирование нужно запомнить (или записать в шпаргалку) пять несложных формул:
(c ⋅ f)′ = c ⋅ f′
(u v)′ = u′ v′
(u — v)′ = u′ — v′
(u ⋅ v)′ = u′v v′u
(u/v)’ = (u’v — v’u)/v2
В данном случае u, v, f — это функции, а c — константа (любое число).
С константой все просто — ее можно смело выносить за знак производной. Специально запоминать придется лишь формулы, где требуется разделить одну функцию на другую или перемножить их и найти производную от результата.
Например: требуется найти производную функции y = (5 ⋅ x3).
y′ = (5 ⋅ x3)′
Вспомним, что константу, а в данном случае это 5, можно вынести за знак производной:
y′ = (5 ⋅ x3)’ = 5 ⋅ (x3)′ = 5 ⋅ 3 ⋅ х3-1 = 15х2
Попробуйте самостоятельно решить эти примеры. Правильные ответы найдете в конце статьи:
Правила вычисления производных
Вычисление производных основано на применении следующих правил, которые мы будем использовать без доказательств, поскольку доказательства выходят за рамки школьного курса математики.
Правило 1 (производная от произведения числа на функцию). Справедливо равенство
(c f (x))’ = c f ‘ (x) ,
где c – любое число.
Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.
Правило 2 (производная суммы функций). Производная суммы функций вычисляется по формуле
(f (x) g (x))’ = f ‘ (x) g’ (x),
то есть производная от суммы функций равна сумме производных этих функций.
Правило 3 (производная разности функций). Производная разности функций вычисляется по формуле
(f (x) – g (x))’ = f ‘ (x) – g’ (x),
то есть производная от разности функций равна разности производных этих функций.
Правило 4 (производная произведения двух функций). Производная произведения двух функций вычисляется по формуле
(f (x) g (x))’ ==f ‘ (x) g (x) f (x) g’ (x),
Другими словами, производная от произведения двух функций равна производной от первой функции, умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.
Правило 5 (производная частного двух функций). Производная от дроби (частного двух функций) вычисляется по формуле
Определение. Рассмотрим функции f (x) и g (x) . Сложной функцией или «функцией от функции» называют функцию вида
f (g (x))
При этом функцию f (x) называют внешней функцией, а функцию g (x) – внутренней функцией.
Правило 6 (производная сложной функции). Производная сложной функции вычисляется по формуле
[ f (g (x))]’ = f ‘ (g (x)) g’ (x)
Другими словами, для того, чтобы найти производную от сложной функции f (g (x)) в точке x нужно умножить производную внешней функции, вычисленную в точке g (x) , на производную внутренней функции, вычисленную в точке x .
Правила дифференцирования сложных функций
Конечно, далеко не все функции выглядят так, как в вышеуказанной таблице. Как быть с дифференцированием, например, вот таких функций: y = (3 2×2)4?
Сложной функцией называют такое выражение, в котором одна функция словно вложена в другую. Производную сложной функции f(y) можно найти по следующей формуле: (f(y))′ = f′(y) ⋅ y′. Другими словами, нужно умножить производную, условно говоря, внешней функции на производную внутренней. |
Пример 1
Найдем производную функции y(x) = (3 2×2)4.
Заменим 3 2×2 на u и тогда получим y = u4.
Согласно приведенному выше правилу дифференцирования сложных функций у нас получится:
y = y′u ⋅ u′x = 4u3 ⋅ u’x
А теперь выполним обратную замену и подставим исходное выражение:
4u3 ⋅ u′x = 4 (3 2×2)3 ⋅ (3 2×2)′ = 16 (3 2×2)3 ⋅ х
Пример 2
Найдем производную для функции y = (x3 4) cos x.
Для дифференцирования этой функции воспользуемся формулой (UV)′ = U′V V′U.
y′ = (x3 4)′ ⋅ cos x (x3 4) ⋅ cos x′ = 3×2 ⋅ cos x (x3 4) ⋅ (-sin x) = 3×2 ⋅ cos x – (x3 4) ⋅ sin x
Таблица производных сложных функций
В следующей таблице приведены формулы для производных сложных функций.
В отдельных строках (с желтым фоном) приведены формулы для производных сложных функций в случае, когда внутренняя функция является линейной функцией и имеет вид f (x) = kx b , где k и b – любые числа, ![]()
| Функция | Формула для производной |
y = (kx b) c , где c – любое число. | y’ = kc (kx b) c – 1 , |
y = ( f (x)) c , где c – любое число. | |
| y = ekx b | y = kekx b |
| y = e f (x) | |
y = akx b где a – любое положительное число, не равное 1 | 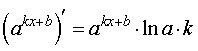 |
y = a f (x) где a – любое положительное число, не равное 1 | |
| y = ln (kx b) , kx b > 0 | 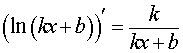 , ,kx b > 0 |
| y = ln ( f (x)) , f (x) > 0 | 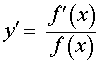 , ,f (x) > 0 |
y = log a (kx b) , kx b > 0 где a – любое положительное число, не равное 1 | 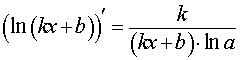 , kx b > 0 , kx b > 0 |
y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 | 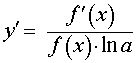 , f (x) > 0 , f (x) > 0 |
| y = sin (kx b) | y’ = k cos (kx b) |
| y = sin ( f (x)) | |
| y = cos (kx b) | y’ = – k sin (kx b) |
| y = cos ( f (x)) | |
y = tg (kx b), где | 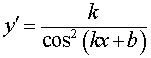 , , 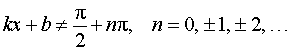 , , |
y = tg ( f (x)), где | 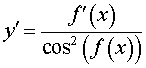 , , 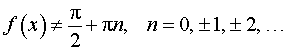 , , |
y = ctg (kx b), где | 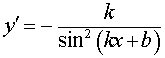 , , |
y = ctg ( f (x)), где | 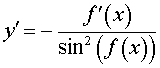 , , |
| y = arcsin (kx b), | 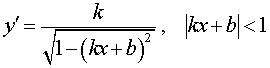 |
| y = arcsin ( f (x)), | 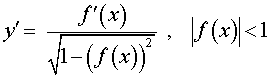 |
| y = arccos (kx b), | 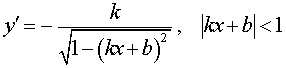 |
| y = arccos ( f (x)), | 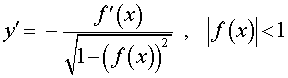 |
| y = arctg (kx b) | 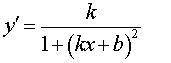 |
| y = arctg ( f (x)) | 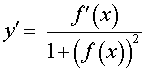 |
| y = arcctg (kx b) | 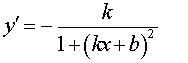 |
| y = arcctg ( f (x)) | 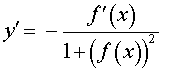 |
Функция: y = (kx b) c , где c – любое число. Формула для производной: y’ = kc (kx b) c – 1 , |
Функция: y = ( f (x)) c , где c – любое число. Формула для производной:
|
Функция: y = ekx b Формула для производной: y = kekx b |
Функция: y = e f (x) Формула для производной:
|
Функция: y = akx b где a – любое положительное число, не равное 1 Формула для производной:
|
Функция: y = a f (x) где a – любое положительное число, не равное 1 Формула для производной:
|
Функция: y = ln (kx b) , kx b > 0 Формула для производной:
|
Функция: y = ln ( f (x)) , f (x) > 0 Формула для производной:
|
Функция: y = log a (kx b) , kx b > 0 где a – любое положительное число, не равное 1 Формула для производной:
|
Функция: y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 Формула для производной:
|
Функция: y = sin (kx b) Формула для производной: y’ = k cos (kx b) |
Функция: y = sin ( f (x)) Формула для производной:
|
Функция: y = cos (kx b) Формула для производной: y’ = – k sin (kx b) |
Функция: y = cos ( f (x)) Формула для производной:
|
Функция: y = tg (kx b), где Формула для производной:
|
Функция: y = tg ( f (x)), где Формула для производной:
|
Функция: y = ctg (kx b), где Формула для производной:
|
Функция: y = ctg ( f (x)), где Формула для производной:
|
Функция: y = arcsin (kx b), Формула для производной:
|
Функция: y = arcsin ( f (x)), Формула для производной:
|
Функция: y = arccos (kx b), Формула для производной:
|
Функция: y = arccos ( f (x)), Формула для производной: |
Функция: y = arctg (kx b) Формула для производной:
|
Функция: y = arctg ( f (x)) Формула для производной:
|
Функция: y = arcctg (kx b) Формула для производной:
|
Функция: y = arcctg ( f (x)) Формула для производной:
|
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Таблица производных часто встречающихся функций
В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.
| Функция | Формула для производной | Название формулы |
y = c , где c – любое число | y’ = 0 | Производная от постоянной функции |
y = x c , где c – любое число | y’ = c xc – 1 | Производная степенной функции |
| y = e x | y’ = e x | Производная от экспоненты (показательной функции с основанием e) |
y = a x где a – любое положительное число, не равное 1 | y’ = a x ln a | Производная от показательной функции с основанием a |
| y = ln x , x > 0 | 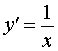 , x > 0 , x > 0 | Производная от натурального логарифма |
y = log a x , x > 0 где a – любое положительное число, не равное 1 | 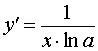 , x > 0 , x > 0 | Производная от логарифма по основанию a |
| y = sin x | y’ = cos x | Производная синуса |
| y = cos x | y’ = – sin x | Производная косинуса |
y = tg x ,
| 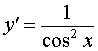 , , 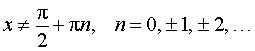 , , | Производная тангенса |
y = ctg x ,
| 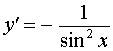 , , | Производная котангенса |
y = arcsin x , | 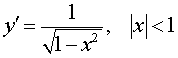 | Производная арксинуса |
y = arccos x , | 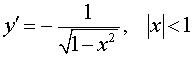 | Производная арккосинуса |
| y = arctg x | 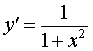 | Производная арктангенса |
| y = arcctg x | 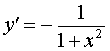 | Производная арккотангенса |
| Производная от постоянной функции |
Функция: y = c , где c – любое число Формула для производной: y’ = 0 |
| Производная степенной функции |
Функция: y = x c , где c – любое число Формула для производной: y’ = c xc – 1 |
| Производная от экспоненты (показательной функции с основанием e) |
Функция: y = e x Формула для производной: y’ = e x |
| Производная от показательной функции с основанием a |
Функция: y = a x где a – любое положительное число, не равное 1 Формула для производной: y’ = a x ln a |
| Производная от натурального логарифма |
Функция: y = ln x , x > 0 Формула для производной:
|
| Производная от логарифма по основанию a |
Функция: y = log a x , x > 0 где a – любое положительное число, не равное 1 Формула для производной:
|
| Производная синуса |
Функция: y = sin x Формула для производной: y’ = cos x |
| Производная косинуса |
Функция: y = cos x Формула для производной: y’ = – sin x |
| Производная тангенса |
Функция: y = tg x , где Формула для производной:
|
| Производная котангенса |
Функция: y = ctg x , где
Формула для производной: |
| Производная арксинуса |
Функция: y = arcsin x , Формула для производной:
|
| Производная арккосинуса |
Функция: y = arccos x , Формула для производной:
|
| Производная арктангенса |
Функция: y = arctg x Формула для производной:
|
| Производная арккотангенса |
Функция: y = arcctg x Формула для производной:
|








