- Чем раньше, тем лучше
- . Десятиклассники, вас это тоже касается
- Учите формулы и теоремы
- Определите «потолок» баллов и просчитайте «свои» задания
- Тайминг — ваше тайное оружие
- Пишите пробники
- Избегайте ошибок по невнимательности
- К тяжелым заданиям делайте несколько подходов
- Участвуйте в олимпиадах
- Подготовка к егэ по математике (профильный уровень): задания, решения и объяснения
- Принцип 1. «заложите крепкий фундамент»
- Принцип 2. «создайте четкий алгоритм»
- Принцип 3 «много практики»
- Принцип 4 «эффективные методы»
- Принцип 5 «работа над ошибками»
- Советы эксперта: как сдать егэ по профильной математике
Чем раньше, тем лучше
Выпускникам 2022 и 2023 годов выпуска советую начинать готовиться как можно раньше, поскольку с 2022 года ЕГЭ по профильной математике будут сдавать по принципиально новым вариантам КИМов. ФИПИ опубликовал перспективные модели совершенно новых заданий.
Осложнит подготовку то, что ни в открытом банке ФИПИ, ни на известных ресурсах РешуЕГЭ и «Незнайка» тренировочные варианты пока никто не разместил. Первое время, пока будут происходить обновления на интернет-ресурсах, мы можем готовиться к ЕГЭ по новым заданиям, используя только одну единственную демоверсию. Выпускникам 2023 года, которые в сентябре пойдут в 10 класс, тоже лучше не терять время и начать готовиться заранее.
Что разработчики ФИПИ предлагают поменять в КИМ ЕГЭ по профильной математике? В опубликованной перспективной модели 2022 года мы видим принципиально новые форматы заданий: № 10 (из блока «Элементы комбинаторики, статистики и теории вероятностей») и № 11 (задание на комплексные числа).
Кстати, задания по профильной математике не меняли так кардинально уже 6 лет. Этот экзамен для ФИПИ так долго был неприкасаемым, поскольку он и так был сложным в плане получения высоких баллов.
. Десятиклассники, вас это тоже касается
Начинайте готовиться к ЕГЭ по профильной математике сейчас. Обновлённые задания абсолютно по всем предметам, долгий дистант, бешеный рост конкурса на бюджетные места в топовых вузах — всё это говорит о том, что выдержать конкуренцию смогут только самые подготовленные и мудрые абитуриенты. Те, кто подстелил соломку заранее.
Еще раз приглашаю на наши очные курсы ЕГЭ Lancman School в Москве и онлайн-курсы в любом регионе страны.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Учите формулы и теоремы
Выучить сразу все формулы и теоремы нереально. Поэтому разместите их рядом с рабочим местом дома и учите постепенно. Помните, что на реальном экзамене одна выученная теорема может сэкономить вам примерно 10-20 минут. В стрессовой ситуации примерно столько времени нужно, чтобы вспомнить то, что не было заучено на этапе подготовки.
Определите «потолок» баллов и просчитайте «свои» задания
У ЕГЭ по профильной математике есть своя специфика и свои уникальные лайфхаки. Низкий средний балл, который мы наблюдаем каждый год, связан с высочайшей сложностью заданий с развёрнутыми ответами. На этапе подготовки подсчитайте, какие баллы ЕГЭ вы ожидаете увидеть в личном кабинете после экзамена.
Потом просчитайте, какие правильно решённые задания помогут вам набрать именно такое количество баллов. Вы же любите математику? Значит, сможете это сделать. Не стремитесь решить весь вариант (хотя постараться стоит). Создайте уникальный алгоритм достижения желаемого результата, выписав те номера заданий, которые в сумме приведут вас к ожидаемым баллам.
Тайминг — ваше тайное оружие
Каждый второй высокобалльник после реального ЕГЭ по профильной математике жалуется, что ему не хватило времени. Если вы последуете совету № 4, обязательно засеките, сколько времени вам надо на выполнение всех заданий, которые вы будете точно решать на ЕГЭ для получения определённого количества баллов.
Пишите пробники
Шестой пункт вытекает из пятого. Проходите пробники как можно чаще. Обязательно фиксируйте не только количество набранных баллов, но и типичные ошибки. Пробные экзамены старайтесь проходить в реальных боевых условиях: время пробника не должно превышать прописанного в демоверсии, попробуйте решать всё без калькулятора, ни в коем случае не пользуйтесь подсказками и шпаргалками.
Если в вашей школе редко проводят пробные ЕГЭ, обратитесь к репетитору или на курсы подготовки к ЕГЭ с просьбой протестировать вас. Только обязательно заранее обговорите, чтобы после пробника вам предоставили максимально подробный отчёт о том, как вы выполнили задания с развёрнутыми ответами. Без обратной связи эффективность пробных ЕГЭ крайне низка.
Избегайте ошибок по невнимательности
Не хочется пугать вас страшными историями о том, как ежегодно школьники теряют баллы из-за невнимательности или небрежности в вычислениях. Но на ЕГЭ по математике таких печальных историй всегда больше, чем на экзаменах по другим предметам. Это ещё одна специфика ЕГЭ по профильной математике: мало правильно ответить, надо ещё все правильно оформить.
Недостаточно всё решить, надо ещё и убедиться, что вы не допустили никаких ошибок в вычислениях и не вписали в бланк неправильный ответ. Советую читать условия и проверять свои записи как минимум два раза. Если заметите, что у вас при подготовке были ошибки именно по глупости, запомните их, чтобы не наступить на эти грабли на реальном экзамене.
К тяжелым заданиям делайте несколько подходов
В первую очередь это касается заданий на геометрию. Не получилось решить сегодня — попробуйте вернуться к задаче завтра или послезавтра. Топовые задачи подвластны только тем, кто прокачал заранее этот уникальный навык — умение нащупывать правильные идеи решения, казалось бы, нерешаемой задачи. Тем более в новой демоверсии таких задач будет ещё больше, чем раньше.
Участвуйте в олимпиадах
Если вы не просто любите математику, но и кайфуете от осознания того, что можете решать нетривиальные сложные задачи, обязательно попробуйте свои силы на различных олимпиадах. Льготы при поступлении дают победа или призёрство во Всероссийской олимпиаде школьников, а также вузовских олимпиадах Перечня. Обо всех олимпиадах 2021–2022 гг. обязательно буду рассказывать подробно в других статьях.
Практика поступления в университеты 2020 и 2021 годов наглядно показала, что в топовых вузах иногда недостаточно иметь 100 баллов на ЕГЭ, чтобы получить бюджетное место. Бывало, что все без исключения заветные бесплатные места доставались олимпиадникам. Эти выпускники зачисляются в вузы в первую очередь.
Верьте в себя, хорошо готовьтесь, и вы обязательно станете победителем или призёром! Но и про подготовку к ЕГЭ не забывайте: высокие баллы на ЕГЭ по профильной математике понадобятся вам для подтверждения статуса абитуриента льготной категории. Имейте в виду, что в 2021 году, например, победители и призёры олимпиад Перечня должны были получить на ЕГЭ по профильному предмету не менее 75 баллов. Некоторые вузы поднимают эту планку ещё выше — до 85 баллов.
Подготовка к егэ по математике (профильный уровень): задания, решения и объяснения
Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут).
Минимальный порог — 27 баллов.
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
- часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).
 Панова Светлана Анатольевна, учитель математики высшей категории школы, стаж работы 20 лет:
Панова Светлана Анатольевна, учитель математики высшей категории школы, стаж работы 20 лет:
«Для того чтобы получить школьный аттестат, выпускнику необходимо сдать два обязательных экзамена в форме ЕГЭ, один из которых математика. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике разделен на два уровня: базовый и профильный. Сегодня мы рассмотрим варианты профильного уровня».
Задание № 1 — проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 — 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.
Пример 1. В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.
Решение:
1) Найдем количество потраченной воды за месяц:
177 — 172 = 5 (куб м)
2) Найдем сколько денег заплатят за потраченную воду:
34,17 · 5 = 170,85 (руб)
Ответ: 170,85.
Задание № 2 —является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований — это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.
#ADVERTISING_INSERT#
Задание № 2 проверяет умение читать диаграммы.
Пример 2. На рисунке показано изменение биржевой стоимости одной акции добывающей компании в первой половине апреля 2022 года. 7 апреля бизнесмен приобрёл 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько потерял бизнесмен в результате этих операций?
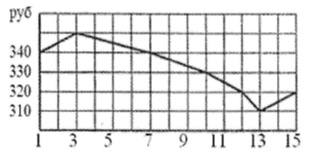
Решение:
1) 340 · 1000 = 340000 (руб) — бизнесмен потратил 7 апреля при покупке 1000 акций.
2) 1000 · 3/4 = 750 (акций) — составляют 3/4 от всех купленных акций.
3) 330 · 750 = 247500 (руб) — бизнесмен получил 10 апреля после продажи 750 акций.
4) 1000 – 750 = 250 (акций) — остались после продажи 750 акций 10 апреля.
5) 310 · 250 = 77500 (руб) — бизнесмен получил 13 апреля после продажи 250 акций.
6) 247500 77500 = 325000 (руб) — бизнесмен получил после продажи 1000 акций.
7) 340000 – 325000 = 15000 (руб) — потерял бизнесмен в результате всех операций.
Ответ: 15000.
Принцип 1. «заложите крепкий фундамент»
Бесконечно жаль тратить время и так очень коротких занятий на отработку простейших, элементарных навыков, но именно они — залог будущего успеха ваших учеников! Парадокс состоит в том, что чем больше времени мы потратим на освоение базового набора знаний, тем больше мы его впоследствии сэкономим при решении более сложных заданий.
Например, я всегда очень долго и кропотливо учу ребят решать элементарные тригонометрические уравнения, доводя их навыки до автоматизма. Но как только этот с материал станет понятнее, чем дважды два, мы с фантастической скоростью разбираем методы решения более сложных задач.
И здесь открывается настоящий простор для экономии времени, как за счет скорости работы с простейшими заданиями, которые всегда встречаются «внутри» сложных, так и за счет возможности разбирать исключительно методы, оставляя их техническую реализацию на дом.
У данного принципа есть и еще одна положительная черта: ребята не только набивают руку, но и приобретают уверенность в себе, своих знаниях и силах, перестают считать себя гуманитариями и начинают действительно понимать предмет.
Принцип 2. «создайте четкий алгоритм»
Я не раз готовила к ЕГЭ выпускников, не знающих таблицу умножения, не умеющих складывать дроби и не знающих ничего толкового о действиях с отрицательными числами, но ни разу в жизни мне не попадались дети, не умеющие решать квадратные уравнения. И дело тут не в том, что это самый простой раздел математики, а в четкой последовательности действий и большом количестве практики. Когда у ученика есть инструкция по работе с тем или иным заданием, шаги которой он понимает, то успех неизбежен!
Для ребят с техническим складом ума соблюдение определенного алгоритма столь же естественно как дыхание. А более творческим натурам они помогут собраться с мыслями, не потерять нить решения и контролировать свои действия на каждом шаге.
Чем ниже уровень ваших учеников, тем проще и конкретнее должна быть описана последовательность действий. Например, один и тот же алгоритм нахождения наибольшего значения функции для учащихся с разным уровнем подготовки можно записать как в две строчки, так и на страницу текста.
Принцип 3 «много практики»
Вопрос с закреплением новых знаний на практике стоит в школе очень остро. Сложные задачи с развернутыми решением, как правило, требуют много времени. Если класс не профильный, то качественно проработать большой объем материала «от и до» за занятие практически нереально.
Такой подход, кроме экономии времени, позволяет ученикам сконцентрировать все внимание на методе решения и особенностях данного задания, не отвлекаясь на уже знакомые и отработанные действия. Количество заданий, прорешенных за урок, существенно увеличивается.
Принцип 4 «эффективные методы»
Качество подготовки к экзаменам во многом зависит от методики преподавателя. Я всегда руководствуясь принципом Парето о том, всего 20% знаний дают 80% результата. Поэтому первостепенной задачей является классификация заданий, выбор наиболее распространенных типов и отбор наиболее эффективных методов их решений.
К сожалению, многие полезные приемы, существенно облегчающие процесс решения и экономящие уйму времени, не входят в школьную программу. Например, метод рационализации, который серьезно упрощает работу со сложными логарифмическими, показательным и другими типами неравенств, изучается только в сильных физмат школах.
А между тем он намного легче и проще стандартных преобразований. Его применение не только экономит время, но и сокращает количество случайных ошибок по невнимательности. При этом научиться применять его под силу «троечнику» всего за 1-2 урока. А значит вероятность справиться со сложными задачами профиля у ваших учеников увеличивается в разы.
Принцип 5 «работа над ошибками»
Чтобы качественно подготовиться к ЕГЭ, да и просто освоить математику, нужно научить ребят искать собственные ошибки. Как правило, ученики страдают от невнимательности, часто ошибаются в одних и тех же трудных местах, например, отбрасывая логарифмы с основаниями меньшими единицы забывают поменять знак неравенства или, извлекая корень из числа в квадрате, теряют модуль.
В наших силах «подстелить соломку». Акцентируя внимание ребят на потенциально проблемном месте в ходе решения, раз за разом напоминая, что именно «здесь» стоит быть предельно аккуратным, мы способны существенно снизить частоту таких досадных ошибок. Более того, получая «подозрительные» ответы, знающие свои «слабые» места ученики намного чаще находят ошибки в решении.
Внимание! Мы расскажем о методе рационализации на бесплатном вебинаре «Применение метода рационализации при решении сложных задач ЕГЭ» — регистрируйтесь по ссылке:
Об авторе: Шеина Ксения Игоревна, преподаватель кафедры фундаментальной математики НИУ ВШЭ Нижний Новгород, научный сотрудник лаборатории Топологических методов в динамике. Контакты: группа Онлайн-школы, персональная страница К. Шеиной.
Советы эксперта: как сдать егэ по профильной математике
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет баллПоможем подготовиться, чтобы сдать экзамены на максимуми поступить в топовые вузы на бюджет.Первый урок бесплатно
Что нужно делать школьнику, чтобы получить 100 баллов?
Чтобы получить 100 баллов, надо любить и понимать математику (быть математиком — по сути, по настроению, по образу жизни). Если школьник рассматривает математику как второстепенный предмет, как предмет, который просто необходимо сдать, например, когда речь идет о поступлении на экономические направления, он не сможет получить 100 баллов ни при каком раскладе. Максимальный балл требует, чтобы человек всем своим «нутром и состоянием своего мозга» был ориентирован на математику. Потому что есть задачи, которые требуют четкого, хорошего логического мышления и владения абсолютно всем материалом. В нужный момент необходимо выудить необходимые знания и применить их для решения задачи. Есть такие задачи, на которые натаскать по принципу «делай вот так» просто нельзя (например, задача № 19). Даже если школьник прекрасно знает математику, 100 баллов получить очень сложно. Это единичные случаи.
По вашему опыту преподавания, какие разделы математики самые сложные и вызывают наибольшие затруднения?
Сегодня для школьника самое сложное — это геометрия. К сожалению, культура геометрии в школе просто отсутствует. И еще, конечно, задачи с параметрами. Старшеклассники их панически боятся. Но ученик, который понимает математику, и с этими задачами справляется. Для их решения требуется именно понимание, а все необходимые для этого знания изложены в курсе школьной математики.
А вообще, в любой теме есть простой материал (азы), который лежит в основе задач из первой части ЕГЭ, и сложный материал, который лежит в основе задач второй части. Думаю, что если есть желание, то каждый в состоянии освоить азы любой темы из школьной программы по математике, а вот более глубокое понимание этих тем и умение решать сложные задачи по силам не всем.
Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов
А какие темы можно назвать самыми простыми?
Обычно школьники легко решают линейные и квадратные уравнения, но только в том случае, если в них нет параметра. Так что по темам «Линейная функция» и «Квадратичная функция» есть простые задачи, а есть сложные. И так по любой теме. Можно сформулировать простую задачу, а можно такую, что никто не решит.
Простыми темами можно считать те, на большинство задач по которым можно школьника натаскать. Простая задача — это гарантированно правильно решенная. А про ЕГЭ (особенно про задачи первой части) так вообще нельзя говорить. Например, школьник знает, как решить задачу, но допускает арифметическую ошибку или невнимательно читает условие (ищет одну величину, а для ответа надо еще что-то с ней сделать). В итоге получается неверный ответ. И задача не решена. И не важно, простая она была или сложная.
Присутствует ли на ЕГЭ по математике фактор везения? Возможно ли получить высокий балл, если знаешь предмет на более скромный результат?
Да, это возможно, но только если речь идет о результате в районе 75 баллов или меньше. Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов. Там нужно решать сложные задачи из второй части, а они требуют четкого обоснования решения, что для большинства является непосильным. Здесь должна быть стабильность.
А можно завалить экзамен, если знаешь предмет очень хорошо?
Элементарно. Арифметические ошибки, невнимательное чтение условия задачи и просто паника. Все это приводит талантливых учеников к более скромным результатам.
Что же делать? Есть «формула успеха», которая поможет подготовиться к ЕГЭ по математике?
Учить математику! Не натаскиваться по вариантам ЕГЭ, а систематически учить темы, разбираться, стараться понять. Тогда до многих задач школьник дойдет сам, своим умом, а это и есть залог успешной подготовки и высоких баллов. Математика — это, в первую очередь, понимание, а потом уже формулы и схемы решения. При подготовке методом натаскивания потолок — это 75 баллов. Одна и та же задача, сформулированная просто «с другого конца», натасканного ребенка деморализует. Он не может узнать знакомую задачу, а разобраться в «новой» сам не в состоянии.
Вот, например, задача № 17. Когда она появилась в вариантах диагностических работ, детям в школе начали давать формулы для ее решения. И школьники заучивали эти формулы, сопротивляясь попыткам учителей объяснить, откуда они взялись. Многие действовали методом «я знаю формулу и по ней буду решать». А на самом экзамене в условие внесли незначительное изменение, и ни одна из выученных формул не подходила. Как получить ту, которая позволит решить задачу, дети не знали. Вроде бы решили все 120 вариантов задания № 17, а на ЕГЭ дали 121-й вариант. В итоге те, кто не разбирался, задачу не решили.
Надо выбросить калькулятор и научиться считать без него
До ЕГЭ по математике осталось 3,5 месяца. Как вы посоветуете выпускникам распределить время, чтобы подготовиться наилучшим образом?
Во-первых, выбросить калькулятор и научиться считать без него. Во-вторых, повторить теорию и выучить формулы (именно сейчас, а не перед экзаменом): то есть подготовить базу, а дальше решать задачи. Можно решать из сборников вариантов ЕГЭ, но, к сожалению, там их не очень много и они часто повторяются.
Каждый ребенок ставит для себя определенную планку в зависимости от того, куда собирается поступать и как знает предмет. Если говорить о заданиях второй части ЕГЭ, то во время подготовки необходимо прежде всего обратить внимание на задачи № 13, № 15 и № 17. Их можно научиться решать. Если решение не вызывает проблем, можно переходить к задачам № 14 и № 16.
Задачи № 18 и № 19 — это, конечно, уже очень высокий уровень, но попробовать можно. Если эти задачи идут хорошо, то я не думаю, что надо тратить оставшееся время на курсы. Лучше решить больше задач самостоятельно. Если же возникают проблемы или неуверенность, что вы все решаете верно, не откладывая обращайтесь за помощью. Эффективная стратегия на этот период — решать, решать и решать!
| Задание № 10 | Задача легкая. Здесь важно внимательно читать условие. Внимание на единицы измерения! Все величины подставлять в одних единицах измерения. |
| Задание № 11 | Текстовая задача. Не считаю ее сложной. Обратите внимание на вопрос задачи, что именно спрашивают в условии и в каких единицах измерения необходимо записать ответ. Часто школьники пишут скорость не того пешехода или производительность не той трубы. |
| Задания № 13, № 15 | Задания решаемые, но должна быть база по всем темам алгебры. Особенное внимание необходимо обратить на область определения (в особенности это касается логарифма, тангенса и котангенса). Нужно уметь применять те тождественные преобразования, которые помогут решить задачу, а не заведут в тупик, и знать все формулы наизусть. |
| Задания № 14, № 16 | Задачи по геометрии. Самое сложное в них — это умение доказать. Для этого школьник должен владеть всем материалом планиметрии и стереометрии, знать все теоремы и следствия из них, уметь их доказывать. И еще важен чертеж! Он может либо стать эффективным инструментом и подсказать правильный ход решения, либо, если сделан некорректно, помешать решению задачи. |
| Задание № 17 | Несложная задача. Это задание на умение формализовать текстовую задачу, то есть записать условие задачи в виде уравнений или неравенств (этого же требует и решение задачи № 11). На ЕГЭ под этим номером пока стабильно дают задачу на проценты. Теоретически может быть и задача на поиск оптимального решения, но такие варианты пока встречались только в диагностических работах. После формализации условия получается стандартная математическая задача о нахождении экстремума функции или на нахождение наибольшего (наименьшего) значения функции на отрезке (аналогично задаче № 12). Здесь важно не пользоваться готовыми формулами, а разбираться, почему в этой задаче так, а в другой иначе. Только тогда можно научиться переводить условие текстовой задачи на язык математики. |
| Задание № 18 | Для решения этой задачи необходимо отличное владение предметом. Поможет ее решить знание свойств элементарных функций, умение исследовать функции и строить их графики. Все это есть в школьном курсе математики. |
| Задание № 19 | Это задача для тех, кому интересна математика. В ходе решения может возникнуть необходимость обратиться к любому разделу предмета из программы любого класса. Нужно найти в своей голове и грамотно применить эти знания. В одной задаче может сочетаться арифметическая прогрессия со свойствами делимости чисел и нахождением наибольшего значения. Для решения этой задачи нужно понимать, когда достаточно привести пример, а когда необходимо строгое обоснование. |








