Готовимся к егэ. задача №20. часть 1.
В
ЕГЭ базового уровня есть задача на
смекалку под №20. Большинство таких
задач решаются довольно просто.
Распределим задачи, представленные в
открытом банке ЕГЭ по типам и дадим им
условное название:
Рассмотрим
первые четыре типа.
Тип
1.
Кузнечик прыгает
вдоль координатной прямой в любом
направлении на единичный отрезок за
один прыжок. Кузнечик начинает прыгать
из начала координат. Сколько существует
различных точек на координатной прямой,
в которых кузнечик может оказаться,
сделав ровно 11 прыжков?
Решение.Заметим,
что кузнечик в
итоге может
оказаться только в точках с нечётными
координатами, так какколичество прыжков, которое он делает,
нечётно.
Максимально кузнечик может оказаться
в точках, модуль
которых не превышает
одиннадцати. Таким образом, кузнечик
может оказаться в точках: −11, −9, −7, −5,
−3, −1, 1, 3, 5, 7, 9 и 11; всего
12 точек.
Ответ:
12
Задачи
для самостоятельного решения.
Тип
2.
Задача
1.Улитка за день заползает вверх по
дереву на 4 м, а за ночь сползает на 3 м.
Высота дерева 10 м. За сколько дней улитка
впервые доползёт до вершины дерева?
Решение.
За день улитка заползёт на 4 метра, а за
ночь — сползёт на 3 метра. Итого за сутки
она заползёт на метр. За шестеро суток
она поднимется на высоту шести метров.
И днём следующего дня она уже окажется
на вершине дерева.
Ответ:
7
Задача
2. Нефтяная компания бурит скважину для
добычи нефти, которая залегает, по данным
геологоразведки, на глубине 3 км. В
течение рабочего дня бурильщики проходят
300 метров в глубину, но за ночь скважина
вновь «заиливается», то есть заполняется
грунтом на 30 метров. За сколько рабочих
дней нефтяники пробурят скважину до
глубины залегания нефти?
Решение.
За день скважина увеличивается на 300 −
30 = 270 м. К началу одиннадцатого рабочего
дня нефтяники пробурят 2700 метров. За
одиннадцатый рабочий день нефтяники
пробурят ещё 300 метров, то есть дойдут
до глубины 3 км.
Ответ:11
Задача
3. В результате паводка котлован заполнился
водой до уровня 2 метра. Строительная
помпа непрерывно откачивает воду,
понижая её уровень на 20 см в час.
Подпочвенные воды, наоборот, повышают
уровень воды в котловане на 5 см в час.
За сколько часов работы помпы уровень
воды в котловане опустится до 80 см?
Решение.
За
час уровень воды в котловане уменьшается
на 20 − 5 = 15 см. Нужно откачать 2 · 100
− 80 = 120 см воды. Следовательно, уровень
воды в котловане опустится до 80 см за 120
: 15 = 8 часов.
Ответ:
8
Задача
4. В бак объёмом 38 литров каждый час,
начиная с 12 часов, наливают полное ведро
воды объёмом 8 литров. Но в днище бака
есть небольшая щель, и из неё за час
вытекает 3 литра. В какой момент времени
(в часах) бак будет заполнен полностью.
Решение.
К
концу каждого часа объём воды в баке
увеличивается на 8 − 3 = 5 литров. Через
6 часов, то есть в 18 часов, в баке будет
30 литров воды. В 18 часов в бак дольют 8
литров воды и объём воды в баке станет
равным 38 литров.
Ответ:
18
Решите
самостоятельно.
Тип
3.
Задача
1. Саша пригласил Петю в гости, сказав,
что живёт в седьмом подъезде в квартире
№ 462, а этаж сказать забыл. Подойдя к
дому, Петя обнаружил, что дом семиэтажный.
На каком этаже живёт Саша? (На всех этажах
число квартир одинаково, номера квартир
в доме начинаются с единицы.)
Решение.
Поскольку в первых 7 подъездах не меньше
462 квартир, в каждом подъезде не меньше
462 : 7 = 66 квартир. Следовательно, на каждом
из 7 этажей в подъезде не меньше 9 квартир.
Пусть
на каждой лестничной площадке по 9
квартир. Тогда в первых семи подъездах
всего 9 · 7 · 7 = 441 квартира, и квартира
462 окажется в восьмом подъезде, что
противоречит условию.
Пусть
на каждой площадке по 10 квартир. Тогда
в первых семи подъездах 10 · 7 · 7 = 490
квартир, а в первых шести — 420. Следовательно,
квартира 462 находится в седьмом подъезде.
Она в нем 42-ая по счету, поскольку на
этаже по 10 квартир, она расположена на
пятом этаже.
Если
бы на каждой площадке было по 11
квартир, то в первых шести подъездах
оказалось бы 11 · 7 · 6 = 462 квартиры, то
есть 462 квартира в шестом подъезде, что
противоречит условию.
Значит
Саша живёт на пятом этаже.
Ответ:
5
Задача
2. Во всех подъездах дома одинаковое
число этажей, а на каждом этаже одинаковое
число квартир. При этом число этажей в
доме больше числа квартир на этаже,
число квартир на этаже больше числа
подъездов, а число подъездов больше
одного. Сколько этажей в доме, если всего
в нём 110 квартир?
Решение.
Число квартир, этажей и подъездов может
быть только целым числом.
Заметим,
что число 110 делится на 2, 5 и 11. Следовательно,
в доме должно быть 2 подъезда, 5 квартир
и 11 этажей.
Ответ:
11
Решите
самостоятельно.
Тип
4.
В обменном пункте можно совершить
одну из двух операций:
У
Николая были только серебряные монеты.
После нескольких посещений обменного
пункта серебряных монет у него стало
меньше, золотых не появилось, зато
появилось 50 медных. На сколько уменьшилось
количество серебряных монет у Николая?
Решение.
Пусть Николай сделал сначала х операций
второго типа, а затем у операций
первого типа. Так как после нескольких
операций золотых монет не осталось, а
количество
медных монет увеличилось на 50, составим
и решим систему уравнений:
Тогда
серебряных монет стало на 3у -5х = 90 – 100
= -10 то есть на 10 меньше.
Ответ:
10
Решите
самостоятельно.
Кузнечик прыгает вдоль координатной прямой – как решать
Формулировка задачи: Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно N прыжков, начиная прыгать из начала координат?
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 20 (Задачи на смекалку).
Рассмотрим, как решаются подобные задачи на примере.
Пример задачи:
Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 6 прыжков, начиная прыгать из начала координат?
Решение:
Чтобы решить данную задачу попробуем рассмотреть все возможные пути кузнечика, которые содержат ровно 6 прыжков из начала координат.
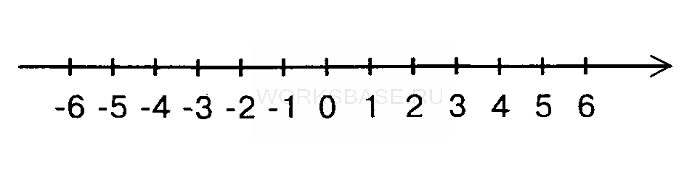
Для этого рассмотрим все варианты, сколько прыжков влево и вправо за весь путь может сделать кузнечик. Порядок прыжков нам не важен, важна лишь итоговая точка.
Первый вариант: 6 прыжков вправо. Кузнечик окажется в точке 6.
Второй вариант: 5 прыжков вправо, 1 прыжок влево. Кузнечик окажется в точке 4.
Третий вариант: 4 прыжка вправо, 2 прыжка влево. Кузнечик окажется в точке 2.
Четвертый вариант: 3 прыжка вправо, 3 прыжка влево. Кузнечик окажется в точке 0.
Пятый вариант: 2 прыжка вправо, 4 прыжка влево. Кузнечик окажется в точке –2.
Шестой вариант: 1 прыжок вправо, 5 прыжков влево. Кузнечик окажется в точке –4.
Седьмой вариант: 6 прыжков влево. Кузнечик окажется в точке –6.
Таким образом, за четное число прыжков кузнечик может оказаться в любой четной точке, таких точек ровно 7. Если бы кузнечик сделал нечетное число прыжков, он бы оказался в любой нечетной точке из возможных.
Ответ: 7
Решу егэ
Заметим, что кузнечик может оказаться только в точках с чётными координатами, поскольку число прыжков, которое он делает, — чётно. Максимально кузнечик может оказаться в точках, модуль которых не превышает двенадцати. Таким образом, кузнечик может оказаться в точках: −12, −10, −8, −6, −4, −2, 0, 2, 4, 6, 8, 10 и 12; всего 13 точек.
Ответ: 13.
Источник: Пробный экзамен Санкт-Петербург 2022. Вариант 1.








