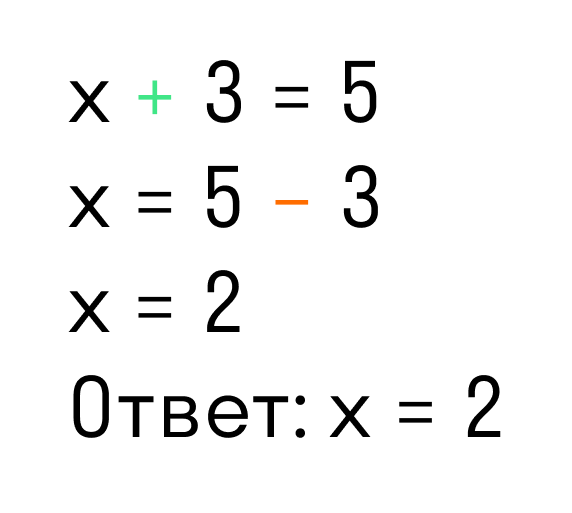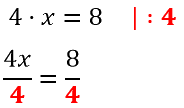Теория для решения заданий 15 по финансовой математике. Аннуитетные и дифференцированные платежи, понятие сложного процента. Основные методы решения задач на проценты.
Цикл уроков про степени и логарифмы и их свойства. Учимся решать показательные и логарифмические уравнения и неравенства. Задания №9 и №15 ЕГЭ по профильной математике.
Знакомимся с понятием степени с натуральным показателем и ее свойствами. Разбор преобразования сложные степенных выражений на примерах.
В уроке разбираем, что такое арифметический квадратный корень и знакомимся с основными его свойствами. Выносим множитель из под знака корня. Избавляемся от иррациональности
Что такое корень n-й степени. Познакомимся со свойствами коня n-й степени и методами оценки значения корня. Разберем какая у него областью определения.
Разбираем, как вычислить степень с рациональным (дробным) показателем. Свойства степени с рациональным показателем. Примеры решения задания №9 из ЕГЭ по математике профильного уровня.
Урок по теме логарифмы и их свойства. Разбираемся, что такое логарифм и какие у него свойства. Научимся считать выражения, содержащие логарифмы. И рассмотри несколько возможных заданий №4 из ЕГЭ по профильной математике.
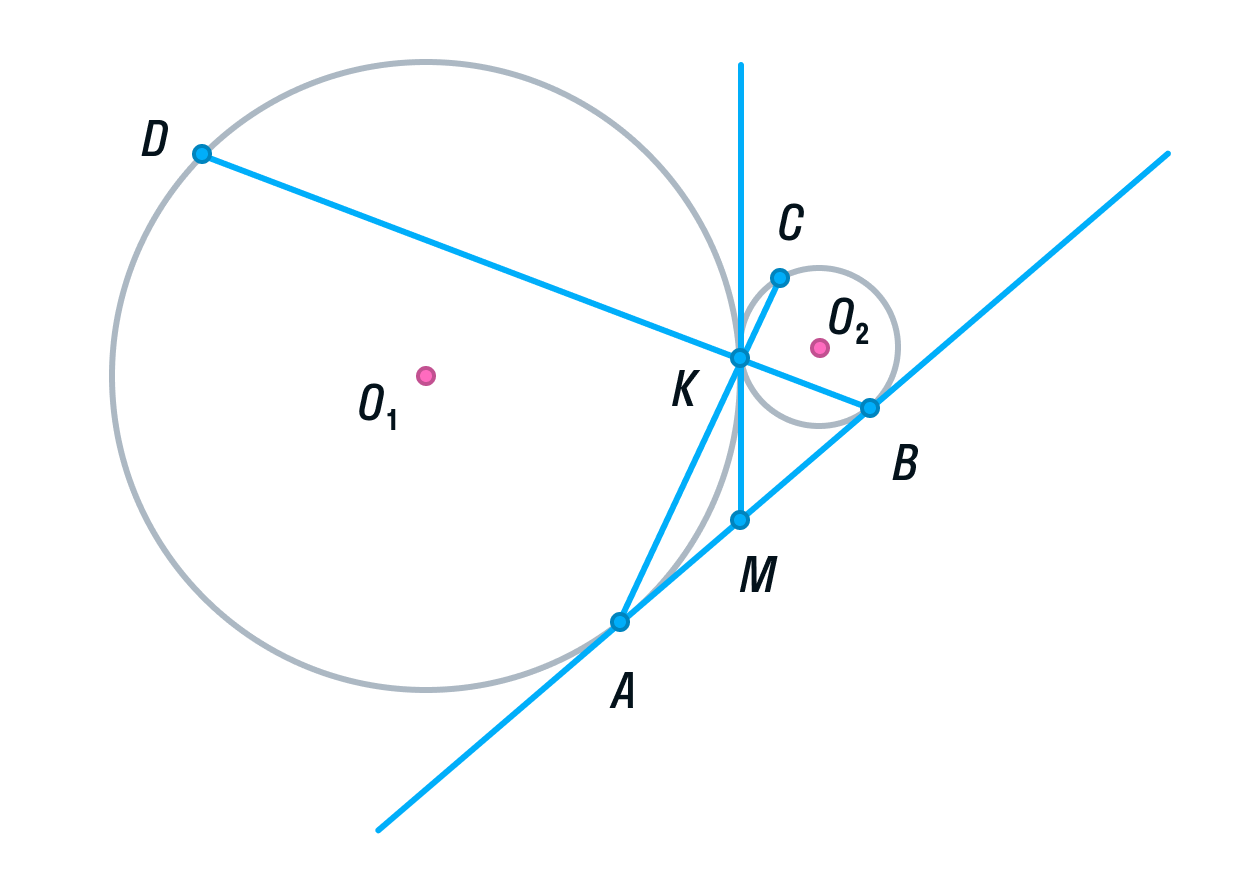
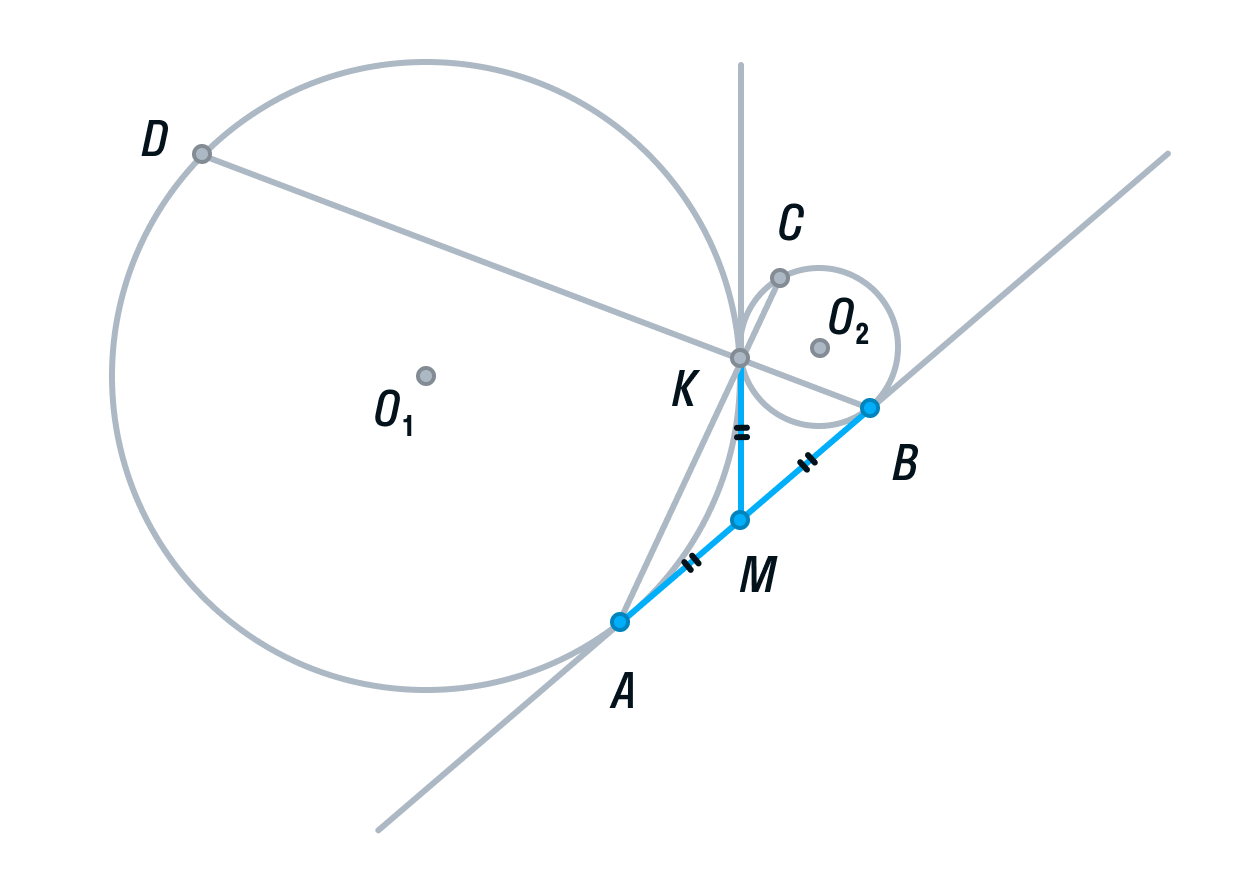
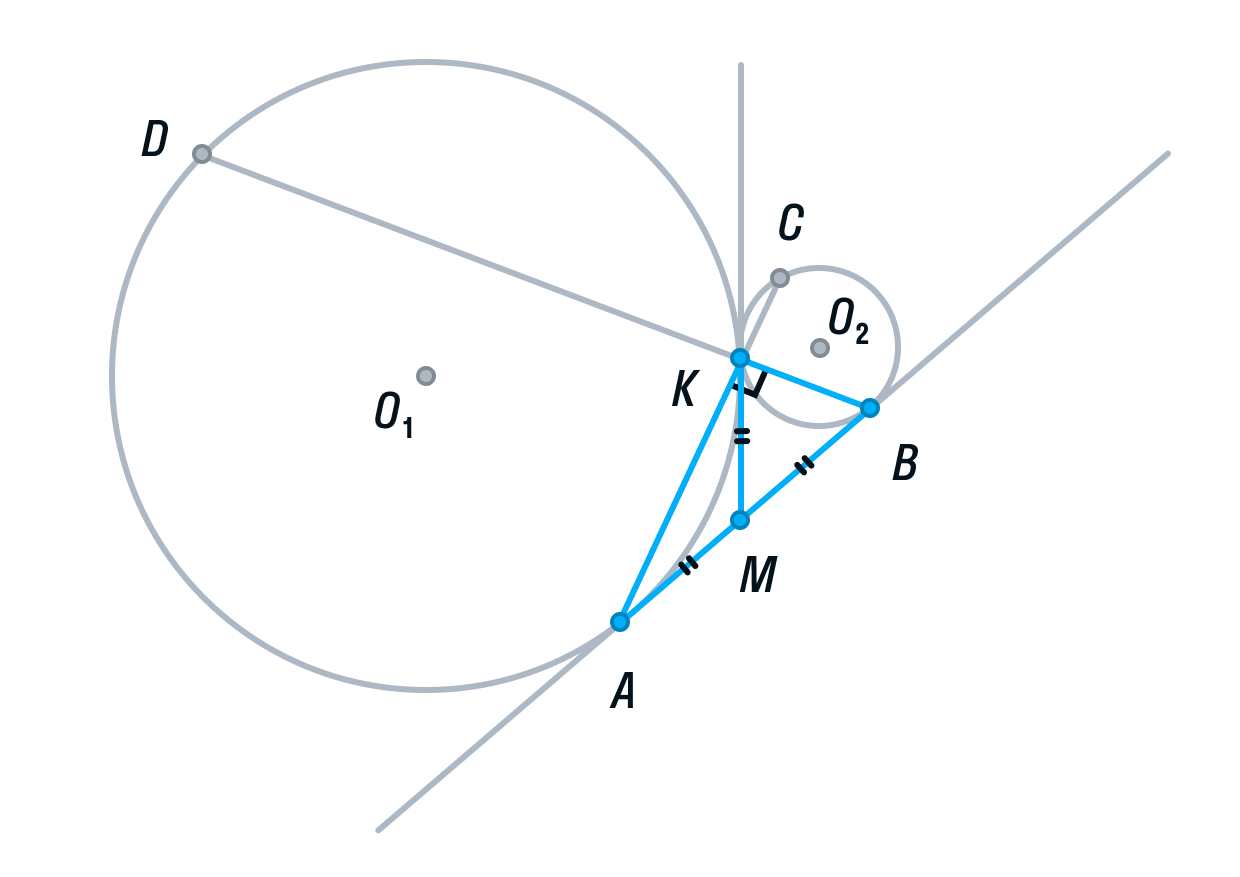
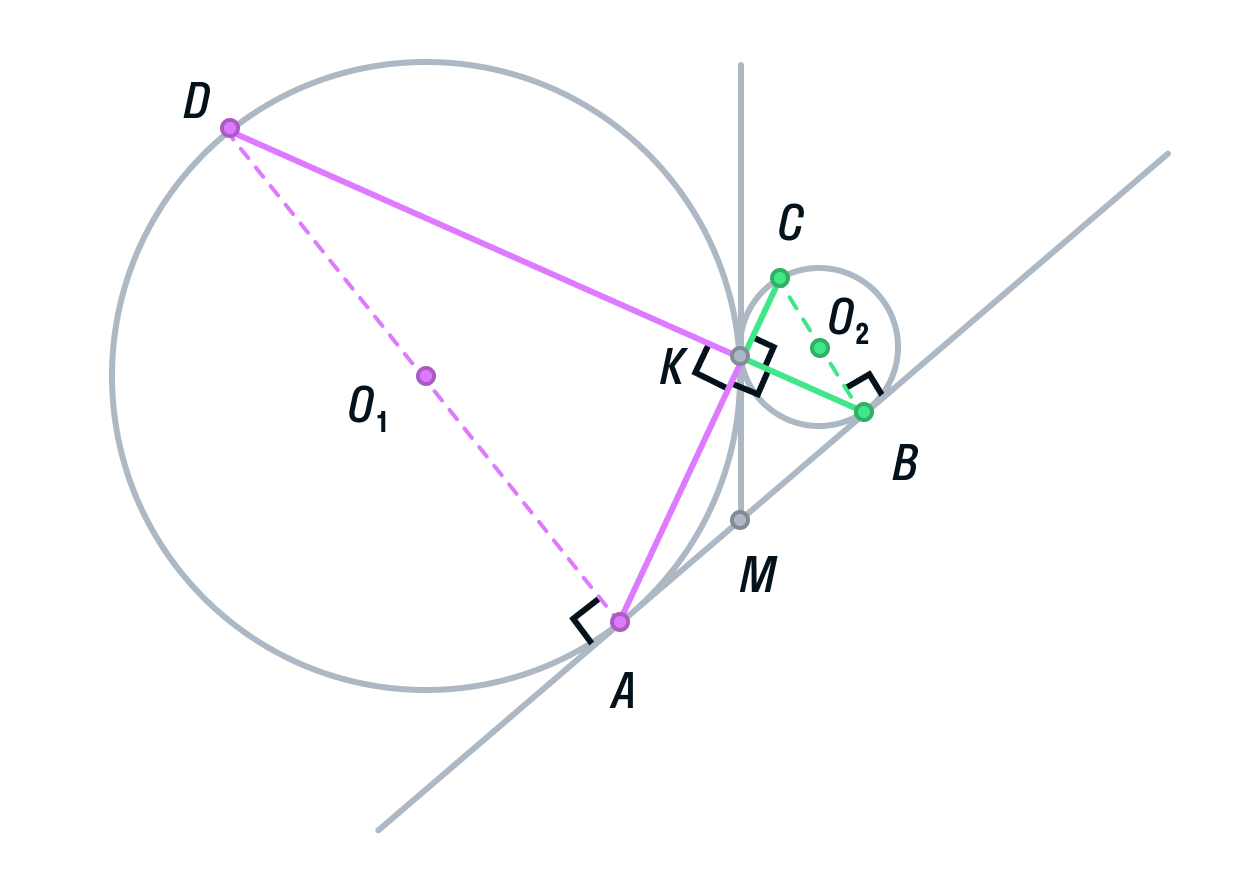
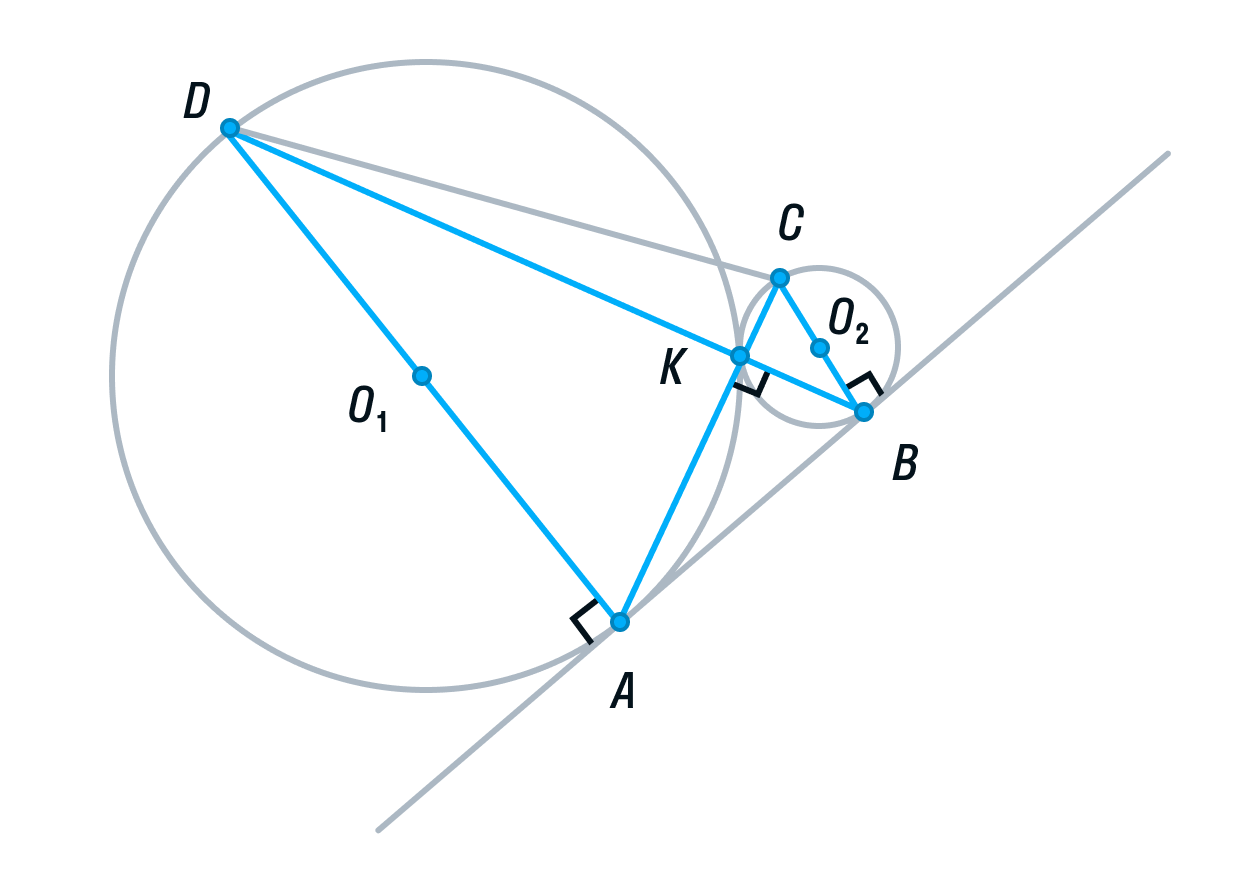
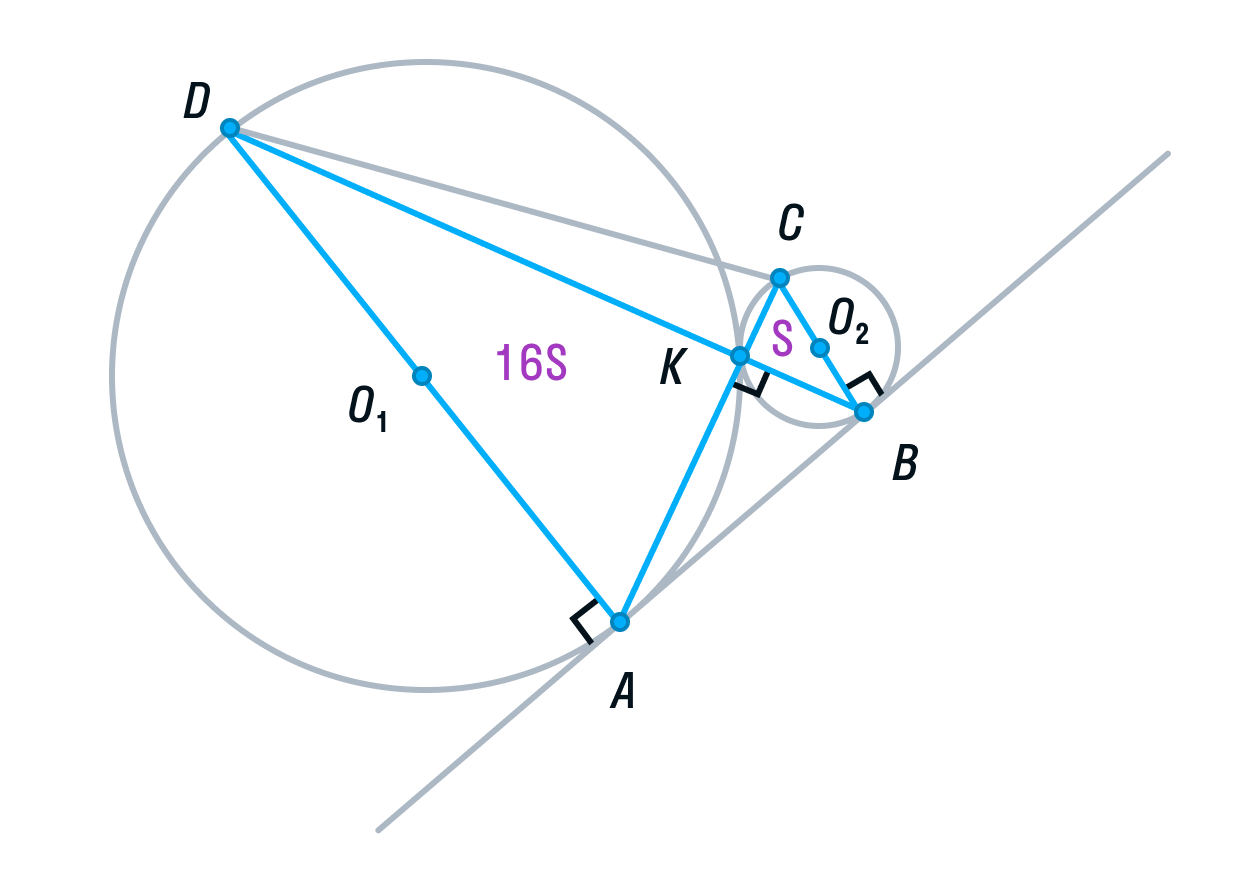
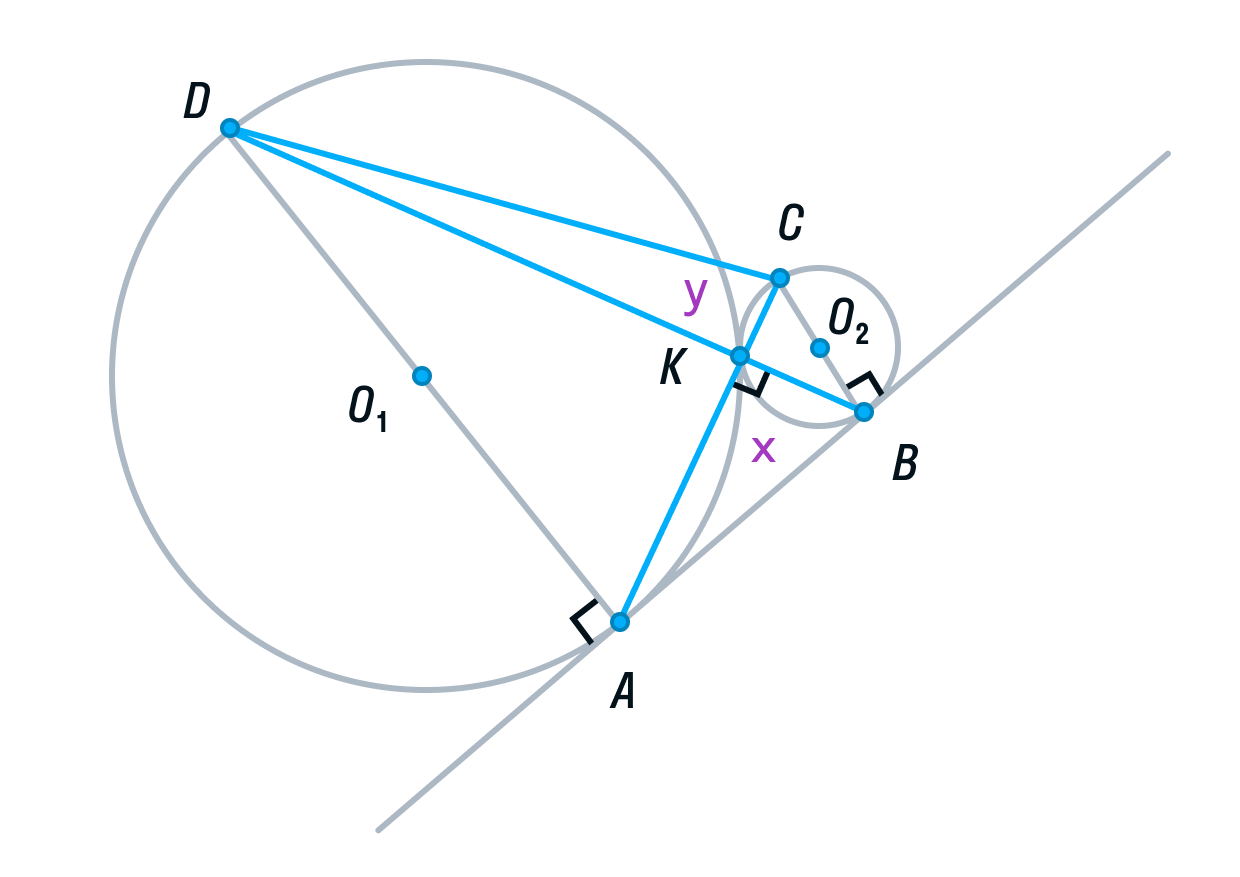
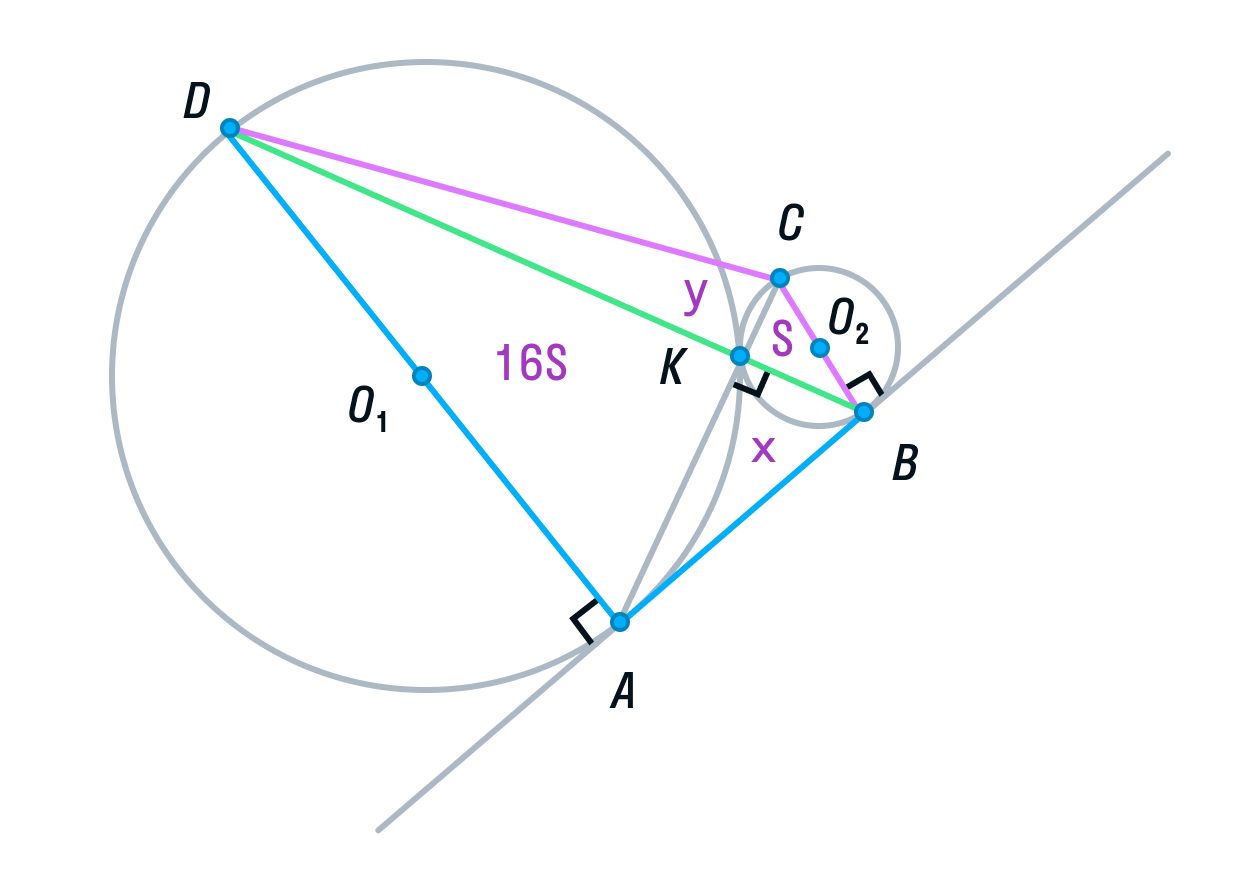
Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.
Закон преломления светового потока на границе раздела двух сред. Явление полного отражения света на границе раздела с оптически более плотной средой.
Подробно разбираем основную теорию про космос необходимую для успешного решения задач по астрономии в ЕГЭ по физике. Также рассмотри несколько основных примеров задания №24 из ЕГЭ.
Частые ошибки, необходимая краткая теория, статистика прошлых лет во 2й части ЕГЭ по математике профильного уровня.
Основные ошибки, что нужно знать, статистика прошлых лет в первой части ЕГЭ по математике профильного уровня.
Чтобы решить квадратное уравнение с параметром, нужно понять, при каких значениях параметра существуют корни, и найти их, выразив через параметр. Обычно это делается просто через анализ дискриминанта. (см. пример 1)
Но иногда в задачах с параметром просят найти такие значения параметра, при которых корни принадлежат определенному числовому промежутку. Например:
- Найдите такие значения параметра, чтобы оба корня были меньше некоторого числа \(γ\): \(x_1≤x_2<γ\).
- Только один из корней принадлежит какому-то промежутку \((γ;β):\)
2 случая: \(γ<x_1<β≤x_2;\) или \(x_1≤γ<x_2<β.\) - Некоторое число \(∝\) лежит между корнями: \((x_1<γ<x_2)\).
- И т.д. Условия могут быть различными.
Теперь разберемся, как при помощи математики записать те или иные условия. Разберем условие: \(x_1≤x_2<γ\). Точно такие же рассуждения будут справедливы и для других условий.
- Очевидно, что \(D≥0\), для того, чтобы корни существовали (либо один, либо два корня — то и то нас устраивает – именно поэтому знак неравенства больше либо равно).
- Чтобы некоторое число лежало вне отрезка \((x_1,x_2)\), необходимо рассмотреть два случая: ветки параболы направлены вверх \((a>0)\); ветки параболы направлены вниз \((a<0)\).
- \(a>0\). Значит, между корнями функция принимает отрицательные значения, а вне этого отрезка – положительные. Так как наше число \(γ\) должно по условию лежать вне отрезка \((x_1,x_2)\), то \(f(γ)>0\).
- \(a<0\). Значит, между корнями функция принимает положительные значения, а вне этого отрезка – отрицательные. Так как наше число \(γ\) должно по условию лежать вне отрезка \((x_1,x_2)\), то \(f(γ)<0\).
Используем небольшую хитрость, чтобы описать оба этих условия: \(a*f(γ)>0\). Этим условием мы накладываем ограничение, что наши корни должны лежать слева или справа от числа \(γ\).
В итоге получаем:
если \(a*f(γ)<0\), то \(γ∈(x_1,x_2)\),
если \(a*f(γ)>0\), то \(γ∉(x_1,x_2)\).
Нам осталось наложить условие, чтобы наши корни были слева от числа \(γ\). Здесь нужно просто сравнить положение вершины нашей параболы \(x_0\) относительно \(γ\). Заметим, что вершина лежит между точками \(x_1\) и \(x_2\). Если \(x_0<γ\), то в системе с предыдущими условиями это будет означать, что число \(γ\) лежит справа от отрезка \((x_1,x_2)\) и соответственно удовлетворяет условию задачи \(x_1≤x_2<γ\).
Таким образом, для того, чтобы решить задачу с условием \(x_1≤x_2<γ\) необходимо решить следующую систему:
То, что дискриминант неотрицательный дает нам существование корней. Второе неравенство указывает, что \(γ∉(x_1,x_2)\). И последнее в совокупности с первыми двумя, что оба корня лежат слева от \(γ\).
Аналогичные рассуждения можно провести для любых условий. Настоятельно рекомендую разобраться во всех пунктах и откуда возникает вышеуказанная система неравенств, и вы легко сможете проводить анализ квадратных уравнений с параметром.
Ниже приведена таблица, в которой разобраны все варианты расположения нулей квадратичной функции на числовой прямой и соответствующие им условия. (см. таблицу)
При каких значениях параметра a уравнение
$$a(a+3) x^2+(2a+6)x-3a-9=0$$
имеет более одного корня?
1 случай:
Если \(a(a+3)=0\), то уравнение будет линейным. При \(a=0\) исходное уравнение превращается в \(6x-9=0\), корень которого \(x=1,5\). Таким образом, при \(a=0\) уравнение имеет один корень.
При \(a=-3\) получаем \(0*x^2+0*x-0=0\), корнями этого уравнения являются любые рациональные числа. Уравнение имеет бесконечное количество корней.
$$ f(-2)=(a+1)*4-(a^2+2a)*(-2)-a-1=2a^2+7a+3; $$
$$ f(2)=(a+1)*4-(a^2+2a)*(2)-a-1=-2a^2-a+3; $$
$$ D=(a^2+2a)^2+4(a+1)^2=(a^2+2a+2)^2=(1+(a+1)^2 )^2>0.$$
Подставляем полученные выражения в систему:
После равносильных преобразований получим систему:
Наша задача свелась к исследованию квадратного многочлена:
$$ f(x)=x^2+(2a-1)x+(a^2+5). $$
Обратим внимание, что коэффициент при \(x^2\) положителен, т.е. ветки параболы направлены вверх.
$$ f(-a)≤0 ⇔ a+5≤0 ⇔ a≤-5;$$
Таким образом, при \(a ≤ -5\) мы имеем одно решение:
Рассмотрим линейные уравнения с параметром вида:
$$p(a)x-q(a)=0,$$
где \(p(a)\) и \(q(a)\)- выражения, которые зависят от параметра. Для того, чтобы решить такое уравнение, нужно найти все \(x\) при всех значениях параметра \(a\). Приведем наше уравнение к виду:
$$p(a)x=q(a),$$
Отсюда единственное решение:
\(x=\frac{q(a)}{p(a)}\) при \(p(a)≠0.\)
Если же \(p(a)=0\) и \(q(a)=0\), то решением данного уравнения является любое число. И последний случай, когда \(p(a)=0\),а \(q(a)≠0\), то уравнение не имеет решений.
Замечу, что по некоторым уравнениям сразу невозможно определить, являются ли они линейными. Выполнив некоторые преобразования, вдруг обнаружим, что в уравнении отсутствуют члены с \(x\) в степени большей, чем 1. Если изначально у нас и были старшие степени, то теперь они сократились.
Мы провели анализ линейного уравнения в общем виде, теперь разберем несколько примеров:
Решить уравнение \(ax-5a=7x-3\) при всех возможных \(a\).
Найдите все \(a\), при которых корнем уравнения $$ax+5a-2(3x+2)=-5x+a^2$$ будет любое число.
Из ОДЗ видно, что \(5a+x≠0\) и \(x-5a≠0,\) таким образом, \(x≠±5a.\)
Приведем уравнение к общему знаменателю \(x^2-25a^2\) и умножим на него все уравнение:
$$x^2-5ax-x^2-10ax-25a^2=-100a^2$$
$$-15ax=-75a^2$$
$$ax=5a^2.$$
После преобразований получили линейное уравнение.
Первый случай: \(a=0.\) Получаем уравнение \(0*x=0.\) Решениями этого уравнения будет любое число, кроме \(x=0\) (ОДЗ \(x≠±5a\)).
Ответ: При \(a=0\) решениями уравнения будут все действительные числа, кроме \(x=0.\) Если \(a≠0,\) то решений нет.
Показана страница 1 из 56
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
- Решение простых уравнений
- Иррациональные уравнения (со знаком корня)
- Подготовка к ЕГЭ по математике со «Школково» — залог успеха!
- Квадратные и линейные уравнения
- Необходимо запомнить
- Задание 1 – найдите корень уравнения 21-4x=32
- Задание 2 – найдите корень уравнения 25-x = 1/16
- Задание 3 – найдите корень уравнения
- Задание 4 – найдите корень уравнения log3(15-х)=log32
- Задание 5 – найдите корень уравнения log3(3-x)=3
- Задание 7. Найдите корень уравнения log2(14-2x)=2log23
- Задания для самостоятельной работы
- Определение показательного уравнения
- Свойства степеней
- Методы решения показательных уравнений
- Приведение к одинаковому основанию
- Пример 1
- Пример 2
- Приведение к одинаковой степени
- Пример
- Пример 2
- Замена переменной
- Пример
- Пример 2
- Вынесение общего множителя
- Пример 1
- Пример 2
- Из каких частей состоит ЕГЭ по математике в 2023 году
- Структура базового уровня ЕГЭ по математике
- Структура профильного уровня ЕГЭ по математике
- Как сдать ЕГЭ по математике
- Задание 16
- Задание 18
- Как выставляют баллы за ЕГЭ по математике
- Сколько баллов нужно набрать, чтобы получить 3, 4 и 5
- 6 советов от эксперта, как готовиться к ЕГЭ по математике
- Понятие уравнения
- Какие бывают виды уравнений
- Как решать простые уравнения
- Примеры линейных уравнений
Решение простых уравнений
Задание
1
Уровень задания: Равен ЕГЭ
ОДЗ: – произвольное. Решим на ОДЗ:
Умножим левую и правую часть уравнения на 9. После умножения: \(2x = 37\), что равносильно \(x = 18,5\) – подходит по ОДЗ.
Задание
2
Уровень задания: Равен ЕГЭ
ОДЗ: – произвольное. Решим на ОДЗ:
Умножим левую и правую часть уравнения на . После умножения: \(4x = -17\), что равносильно \(x = -4,25\) – подходит по ОДЗ.
Задание
3
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \(x^2 — 11x + 28 = 0\). Если уравнение имеет более одного корня, в ответе укажите больший из них.
ОДЗ: – произвольное. Решим на ОДЗ:
Задание
4
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \(2x^2 — 7x + 3 = 0\). Если уравнение имеет более одного корня, в ответе укажите меньший из них.
ОДЗ: – произвольное. Решим на ОДЗ:
Задание
5
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \((4x + 5)^2 = (4x + 4)^2\).
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем \(16x^2 + 40x + 25 = 16x^2 + 32x + 16\), что равносильно \(8x = -9\), откуда \(x = -1,125\) – подходит по ОДЗ.
Задание
6
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \((5x + 8)^2 = 160x\).
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем \(25x^2 + 80x + 64 = 160x\), что равносильно \(25x^2 — 80x + 64 = 0\), что равносильно \((5x — 8)^2 = 0\), что равносильно \((5x — 8)(5x — 8) = 0\).
Задание
7
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \((2x + 11)^2 = 88x\).
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем \(4x^2 + 44x + 121 = 88x\), что равносильно \(4x^2 — 44x + 121 = 0\), что равносильно \((2x — 11)^2 = 0\), что равносильно \((2x — 11)(2x — 11) = 0\).

Как заходить в аудиторию на ЕГЭ
Как заходить в аудиторию на ЕГЭ
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Иррациональные уравнения (со знаком корня)
Иррациональное уравнение – уравнение, содержащее переменную под знаком корня любой степени.
Стандартное иррациональное уравнение:
Если – четное, то данное уравнение имеет решения только при и ввиду определения корня четной степени. Значит:
(условие автоматически выполняется в данной системе)
Если – нечетное, то данное уравнение имеет решения при любых и . Значит:
Задание
1
Уровень задания: Равен ЕГЭ
ОДЗ: \(x \geq -12\). Решим на ОДЗ:
При возведении в квадрат левой и правой части уравнения в общем случае могут приобретаться лишние корни, но не могут теряться корни исходного уравнения.
Возведём в квадрат левую и правую часть, найдём корни получившегося уравнения и проверим подстановкой, все ли они являются корнями исходного уравнения: \(x + 12 = 36\), что равносильно \(x = 24\).
Задание
2
Уровень задания: Равен ЕГЭ
ОДЗ: \(4x + 5 \geq 0\), что равносильно \(x \geq -1,25\). Решим на ОДЗ:
При возведении в квадрат левой и правой части уравнения в общем случае могут приобретаться лишние корни, но не могут теряться корни исходного уравнения.
Возведём в квадрат левую и правую часть, найдём корни получившегося уравнения и проверим подстановкой, все ли они являются корнями исходного уравнения: \(4x + 5 = 36\), что равносильно \(x = 7,75\).
Задание
3
Уровень задания: Равен ЕГЭ
ОДЗ: \(6 — x \geq 0\), что равносильно \(x \leq 6\). Решим на ОДЗ:
При возведении в квадрат левой и правой части уравнения в общем случае могут приобретаться лишние корни, но не могут теряться корни исходного уравнения.
Возведём в квадрат левую и правую часть, найдём корни получившегося уравнения и проверим подстановкой, все ли они являются корнями исходного уравнения: \(6 — x = 9\), что равносильно \(x = -3\).
Задание
4
Уровень задания: Равен ЕГЭ
При возведении в квадрат левой и правой части уравнения в общем случае могут приобретаться лишние корни, но не могут теряться корни исходного уравнения.
Задание
5
Уровень задания: Равен ЕГЭ
При возведении в квадрат левой и правой части уравнения в общем случае могут приобретаться лишние корни, но не могут теряться корни исходного уравнения.
Задание
6
Уровень задания: Равен ЕГЭ
Задание
7
Уровень задания: Равен ЕГЭ
При возведении в квадрат левой и правой части уравнения в общем случае могут приобретаться лишние корни, но не могут теряться корни исходного уравнения.
При подготовке к ЕГЭ по математике у многих выпускников вызывает трудности решение иррациональных уравнений и неравенств. Вывод переменных из-под знака корня и возведение в степени часто сопровождаются ошибками в вычислениях, поэтому стоит обратить внимание на подобные задания. Мы предлагаем школьникам изучить теоретические материалы, рассмотреть типовые примеры с решениями иррациональных уравнений. Также ученики могут попробовать свои силы в выполнении более сложных задач с неизвестными.
Подготовка к ЕГЭ по математике со «Школково» — залог успеха!
Чтобы легко решать иррациональные уравнения со знаком корня, советуем регулярно заниматься на нашем портале. С помощью «Школково» вы сможете получить всю необходимую теоретическую информацию по теме, а также попрактиковаться в решении типовых задач, которые обязательно будут включены в итоговое тестирование.
Наши преподаватели собрали все полезные материалы, систематизировали и изложили их таким образом, чтобы школьникам было проще вспомнить и усвоить информацию даже по сложным темам. База постоянно обновляется и дополняется новыми упражнениями, поэтому выпускники будут получать и решать задания без повторений.
Мы предлагаем начать с легких уравнений и постепенно переходить к более сложным. Так ученикам проще определить свои слабые стороны и сделать упор на те темы, которые даются сложнее всего.
Если простые примеры не вызывают трудностей, пропускайте несколько упражнений и переходите к уравнениям профильного уровня. При необходимости повторите правила и вернитесь к заданию.
Обратите внимание, что занятия на нашем портале доступны не только старшеклассникам из Москвы, но и учащимся из других городов России.

Как заходить в аудиторию на ЕГЭ
Как заходить в аудиторию на ЕГЭ
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Квадратные и линейные уравнения
если , то оно имеет два различных корня
если , то оно имеет один корень (иногда говорят, что два совпадающих)
если , то оно не имеет корней.
Теорема Виета для квадратного уравнения:
Если квадратное уравнение имеет неотрицательный дискриминант, то сумма корней уравнения
Если квадратное уравнение:
имеет два корня и , то .
имеет один корень (иногда говорят, что два совпадающих), то .
не имеет корней, то квадратный трехчлен никогда не может быть равен нулю. Более того, он при всех строго одного знака: либо положителен, либо отрицателен.
Полезные формулы сокращенного умножения:
Задание
1
Уровень задания: Равен ЕГЭ
ОДЗ: – произвольное. Решим на ОДЗ:
Умножим левую и правую часть уравнения на 9. После умножения: \(2x = 37\), что равносильно \(x = 18,5\) – подходит по ОДЗ.
Задание
2
Уровень задания: Равен ЕГЭ
ОДЗ: – произвольное. Решим на ОДЗ:
Умножим левую и правую часть уравнения на . После умножения: \(4x = -17\), что равносильно \(x = -4,25\) – подходит по ОДЗ.
Задание
3
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \(x^2 — 11x + 28 = 0\). Если уравнение имеет более одного корня, в ответе укажите больший из них.
ОДЗ: – произвольное. Решим на ОДЗ:
Задание
4
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \(2x^2 — 7x + 3 = 0\). Если уравнение имеет более одного корня, в ответе укажите меньший из них.
ОДЗ: – произвольное. Решим на ОДЗ:
Задание
5
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \((4x + 5)^2 = (4x + 4)^2\).
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем \(16x^2 + 40x + 25 = 16x^2 + 32x + 16\), что равносильно \(8x = -9\), откуда \(x = -1,125\) – подходит по ОДЗ.
Задание
6
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \((5x + 8)^2 = 160x\).
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем \(25x^2 + 80x + 64 = 160x\), что равносильно \(25x^2 — 80x + 64 = 0\), что равносильно \((5x — 8)^2 = 0\), что равносильно \((5x — 8)(5x — 8) = 0\).
Задание
7
Уровень задания: Равен ЕГЭ
Найдите корень уравнения \((2x + 11)^2 = 88x\).
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем \(4x^2 + 44x + 121 = 88x\), что равносильно \(4x^2 — 44x + 121 = 0\), что равносильно \((2x — 11)^2 = 0\), что равносильно \((2x — 11)(2x — 11) = 0\).
Знакомство школьника с квадратными уравнениями вида , где , , — заданные числа, происходит еще задолго до сдачи ЕГЭ по математике в Москве или любом другом городе РФ, а именно в 8 классе. Несмотря на то, что на изучение материала по данной теме, как правило, отводится немало времени, далеко не все школьники с легкостью решают подобные задачи. Поэтому, готовясь к сдаче выпускного экзамена, школьникам как в Москве, так и в других населенных пунктах РФ необходимо повторить такой раздел алгебры, как квадратные уравнения: в ЕГЭ по математике они обязательно встретятся.
Для того чтобы освежить в памяти основные способы решения подобного задания и способы решения иррациональных уравнений, воспользуйтесь образовательным проектом «Школково». Наши специалисты подготовили для вас в максимально понятной и доступной форме теоретический материал по теме «Квадратные уравнения», подобрали интересные примеры, которые встречаются в ЕГЭ, а также их подробные решения.
Необходимо запомнить
Для решения квадратных уравнений в ЕГЭ по математике следует выучить формулу, по которой вычисляется дискриминант. Она довольная простая: .
Квадратное уравнение, которое вам предстоит решить в ЕГЭ, может иметь не более двух корней. Если вычисленный дискриминант больше 0, то следует использовать следующие формулы:
Если D = 0, то уравнение имеет один корень (иногда говорят, что 2 равных):
Если дискриминант меньше 0, то уравнение не имеет корней.

Как заходить в аудиторию на ЕГЭ
Как заходить в аудиторию на ЕГЭ
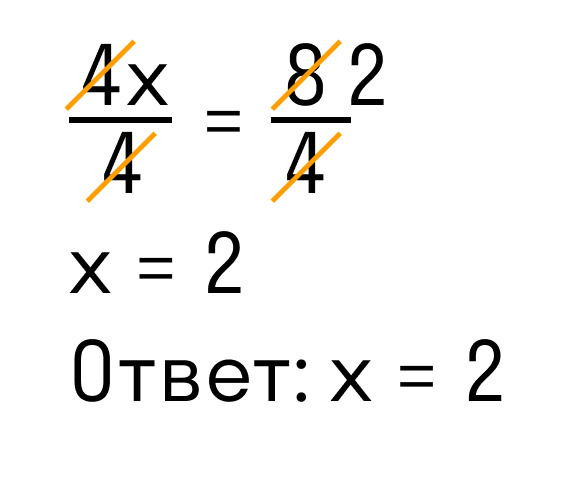
Сегодня мы будем тренировать навык решения задания 5 ЕГЭ – найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним – что значит – найти корень уравнения?
Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.
Например, 3x=9 – это уравнение, а 3.3=9 – это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 – получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.
Вот этим мы и займемся – будем находить корень уравнения.
Задание 1 – найдите корень уравнения 21-4x=32
Это показательное уравнение. Оно решается следующим образом – нужно чтобы и слева, и справа от знака “равно” была степень с одинаковым основанием.
Слева у нас основание степени 2, а справа – степени нет вовсе. Но мы знаем, что 32 – это 2 в пятой степени. То есть, 32=25
Таким образом, наше уравнение будет выглядеть так: 21-4х=25
Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:
Получаем обыкновенное уравнение. Решаем обычным способом – все неизвестные оставляем слева, а известные переносим вправо, получим:
Делаем проверку: 21-4(-1)=32
Мы нашли корень уравнение. Ответ: х=-1.
Самостоятельно найдите корень уравнения в следующих заданиях:
Задание 2 – найдите корень уравнения 25-x = 1/16
Уравнение решаем аналогично – путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае – к основанию степени 2.
Используем следующее свойство степени:
По этому свойству мы получим для правой части нашего уравнения:
Тогда наше уравнение запишется в виде:
Если равны основания степени, значит, равны и показатели степени:
Сделаем проверку – подставим найденное значение х в исходное уравнение – если мы получим верное равенство, значит, мы решили уравнение правильно.
Мы нашли корень уравнения правильно.
Задание 3 – найдите корень уравнения
Заметим, что справа у нас стоит 1/8, а 1/8 – это

Тогда наше уравнение запишется в виде:
Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:
Ответ: х=5. Проверку сделайте самостоятельно.
Задание 4 – найдите корень уравнения log3(15-х)=log32
Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака “равно” были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:
Задание 5 – найдите корень уравнения log3(3-x)=3
Число 3 – это log327. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень – это 27, а сам логарифм – это показатель степени, в которую нужно возвести 3, чтобы получить 27.
Смотрите на картинке:

Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:
Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:
Задание 7. Найдите корень уравнения log2(14-2x)=2log23
Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы Найдите значение выражения и Как решать неравенства .
(ЕГЭ 2023, Досрок)
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Решение: Ответ:
(ЕГЭ 2023, Досрок) а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Ответ: + показать
(ЕГЭ 2023, Досрок)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение Ответ: + показать
(ЕГЭ 2023, Досрок)
а) ) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Ответ: + показать
(ЕГЭ 2023, Пробник)
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Решение Ответ: + показать
(ЕГЭ 2023, Пробник)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Ответ: + показать
(ЕГЭ 2023, Досрок)
а) Решите уравнение: .
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение Ответ: + показать
(ЕГЭ 2023, Досрок)
а) Решите уравнение: .
б) Найдите все корни этого уравнения, принадлежащие отрезку
Ответ: + показать
(ЕГЭ 2023, Статград)
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение Ответ: + показать
(ЕГЭ 2023, Статград)
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Ответ: + показать
(Реальный ЕГЭ, 2021)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Реальный ЕГЭ, 2021)
а) Решите уравнение
б) Найдите его корни на промежутке Решение
(Демо ЕГЭ, 2020)
a) Решите уравнение
б) Найдите его корни на промежутке . Видеорешение
(Реальный ЕГЭ, 2019)
a) Решите уравнение
б) Найдите его корни на промежутке . Решение
(Реальный ЕГЭ, 2019)
a) Решите уравнение
б) Найдите его корни на промежутке . Решение
(Реальный ЕГЭ, 2018)
a) Решите уравнение
б) Найдите его корни на промежутке . Решение
(Досрочный резервный ЕГЭ, 2018)
a) Решите уравнение
б) Найдите его корни на промежутке . Решение
(Досрочный ЕГЭ, 2018)
a) Решите уравнение
б) Укажите все корни этого уравнения, принадлежащие промежутку . Решение
(Резервный ЕГЭ, 2017)
а) Решите уравнение
б) Найдите корни уравнения из отрезка Решение
(Реальный ЕГЭ, 2017)
а) Решите уравнение
б) Найдите корни уравнения из отрезка Решение
(Реальный ЕГЭ, 2017)
а) Решите уравнение
б) Найдите корни уравнения из отрезка Решение
(Досрочн. ЕГЭ, 2017)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Резервн. ЕГЭ, 2016)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р, апрель 2016)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку Решение
(Досрочн. ЕГЭ, 2016)
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие промежутку Решение
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку Решение
a) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие промежутку . Решение
a) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку Решение
a) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку Решение
a) Решить уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Найдите его корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие интервалу Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие интервалу Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Укажите корни уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Укажите корни уравнения, принадлежащие промежутку Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Укажите корни уравнения, принадлежащие промежутку Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Укажите корни уравнения, принадлежащие промежутку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни уравнения, принадлежащие промежутку Решение
(Т/Р А. Ларина)
Найдите все корни уравнения удовлетворяющие неравенству
Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни уравнения, принадлежащие интервалу Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите его корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите его корни из отрезка Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Найдите его корни на отрезке Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Найдите его корни на отрезке Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Найдите его корни, принадлежащие промежутку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Найдите его корни, принадлежащие промежутку Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Найдите его корни, принадлежащие промежутку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Найдите его корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Найдите его корни, принадлежащие промежутку Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Укажите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие интервалу Решение
(Т/Р А. Ларина)
a) Решите уравнение .
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Найдите его корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Найдите его корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Найдите его корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Найдите его корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите его корни из интервала Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите его корни, принадлежащие интервалу Решение
(Т/Р А. Ларина)
a) Решите уравнение .
б) Укажите корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение .
б) Укажите корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Найдите все корни на промежутке Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни, принадлежащие отрезку Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни уравнения, принадлежащие интервалу Решение
(Т/Р А. Ларина)
a) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие интервалу Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Найдите все корни уравнения на отрезке Решение
(Т/Р А. Ларина)
(Т/Р А. Ларина)
а) Решите уравнение
б) Найдите все корни на промежутке (0; 5). Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Найдите все корни на промежутке . Решение
(Т/Р А. Ларина)
а) Решите уравнение .
б) Найдите все корни на промежутке Решение
(Т/Р А. Ларина)
a) Решите уравнение ,
б) Найдите все корни на промежутке . Решение
(Т/Р А. Ларина)
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку . Решение
(Т/Р А. Ларина)
а) Решите уравнение.
б) Укажите корни этого уравнения, принадлежащие промежутку . Решение
(Т/Р А. Ларина)
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
(Т/Р А. Ларина)
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
(Т/Р А. Ларина)
а) Решите уравнение.
б) Укажите его корни из интервала . Решение
(Т/Р А. Ларина)
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
(Т/Р А. Ларина)
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Укажите его корни из отрезка . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите наибольший отрицательный корень. Решение
(Т/Р, 2017) а) Решите уравнение
б) Найдите все его корни, принадлежащие отрезку Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите решения, принадлежащие промежутку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите натуральное число такое, что
где
– корень уравнения. Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку .
(Т/Р А. Ларина)
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку .
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р А. Ларина) Дано уравнение
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку . Решение
(Т/Р 283 А. Ларина) a) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку Решение
Иррациональные выражения, уравнения и неравенства
Простейшие иррациональные уравнения мы рассматривали здесь.

С простейшими иррациональными уравнениями мы сталкиваемся в части В ЕГЭ по математике.
Сегодня же работаем с , с которыми вы можете столкнуться в части С ЕГЭ по математике.
Предлагаю решать уравнения способом равносильных переходов.
смотрите здесь.
Задания для самостоятельной работы
Ответ: + показать
Ответ: + показать
Ответ: + показать
Определение показательного уравнения
Показательными называются уравнения, в которых переменная находится в показателе степени. Простейшее уравнение такого вида: aх = b, где a > 0, a ≠ 1 и ax = ay.
Для решения даже простейших показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс тему «Свойства степенной функции» — советуем повторить ее перед тем, как читать дальнейший материал.
Показательной функцией называют такую: y = ax, где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a < 1 (но больше 0) — непрерывно убывает. Это хорошо видно на рисунке ниже.
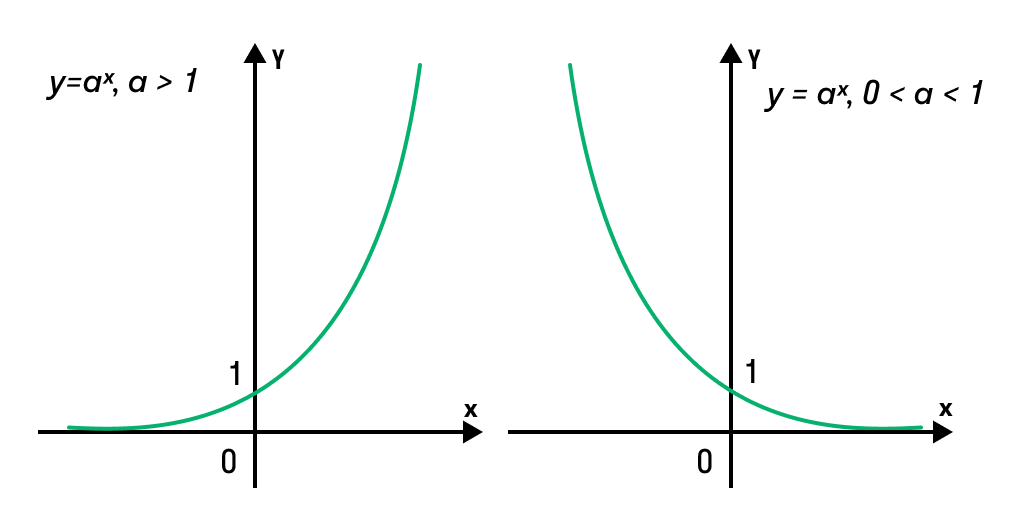
Показательная функция не может быть отрицательным числом, т. е. выражение у = ax при а ≤ 0 корней не имеет.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут решать сложные показательные уравнения.
Как видите, ничего нового здесь нет, все это проходят в 6–7 классе.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту