Задание №9 ЕГЭ по математике профильного уровня ⋆ СПАДИЛО

Содержание

Второй вариант задания (из ященко, №1)
Вычисления и преобразования выражений. задания 9 профильного егэ (часть 1)
Задание 1.
Задание 2.
Задание 3.
Задание 4.
Задание 5
Задание 6
Задание 7
Задание 8
Задание 9
Задания егэ профильного уровня по математике
Как решать 9 задание егэ 2022 математика профиль видео теория:
Первый вариант задания (демонстрационный вариант 2022)
Поделиться
Пятый вариант задания (из ященко)
Решение:
Решу егэ 2022 тригонометрические функции 9 задание профиль математика с ответами:
Степенные выражения
Третий вариант задания (из ященко, №16)
Четвертый вариант задания (из ященко)

Второй вариант задания (из ященко, №1)

[su_note note_color=”#defae6″]

Найдите , если , если Задание №9 ЕГЭ по математике профильного уровня ⋆ СПАДИЛО .

[/su_note]

Вычисления и преобразования выражений. задания 9 профильного егэ (часть 1)

1. Алгебраические выражения

2. Выражения с корнями

3. Логарифмические выражения

4. Выражения со степенями

4.1	Найдите значение выражения 5^{0,36} cdot 25^{0,32}	Смотреть видеоразбор
4.2	Найдите значение выражения frac{3^{6,5}}{9^{2,25}}	Смотреть видеоразбор
4.3	Найдите значение выражения 7^{frac{4}{9}} cdot 49^{frac{5}{18}}	Смотреть видеоразбор
4.4	Найдите значение выражения frac{2^{3,5} cdot 3^{5,5}}{6^4,5}	Смотреть видеоразбор
4.5	Найдите значение выражения 35^{-4,7} cdot 7^{5,7} : 5^{-3,7}	Смотреть видеоразбор
4.6	Найдите значение выражения frac{sqrt[9]{7} cdot sqrt[18]{7}}{sqrt[6]{7}}	Смотреть видеоразбор
4.7	Найдите значение выражения frac{sqrt[5]{10} cdot sqrt[5]{16}}{sqrt[5]{5}}	Смотреть видеоразбор
4.8	Найдите значение выражения (frac{2^{frac{1}{3}} cdot 2^{frac{1}{4}}}{sqrt[12]{2}})^2	Смотреть видеоразбор
4.9	Найдите значение выражения frac{(2^{frac{3}{5}} cdot 2^{frac{2}{3}})^{15}}{10^9}	Смотреть видеоразбор
4.10	Найдите значение выражения 0,8^{frac{1}{7}} cdot 5^{frac{2}{7}} cdot 20^{frac{6}{7}}	Смотреть видеоразбор
4.11	Найдите значение выражения 5 cdot sqrt[3]{9} cdot sqrt[6]{9}	Смотреть видеоразбор
4.12	Найдите значение выражения frac{sqrt[28]{3} cdot 3 cdot sqrt[21]{3}}{sqrt[12]{3}}	Смотреть видеоразбор
4.13	Найдите значение выражения frac{sqrt[15]{5} cdot 5 cdot sqrt[10]{5}}{sqrt[6]{5}}	Смотреть видеоразбор
4.14	Найдите значение выражения 0,75^{frac{1}{8}} cdot 4^{frac{1}{4}} cdot 12^{frac{7}{8}}	Смотреть видеоразбор
4.15	Найдите значение выражения 7^{sqrt{5}-1} cdot 7^{2 sqrt{5}} : 7^{2sqrt{5}-1}	Смотреть видеоразбор
4.16	Найдите значение выражения frac{1}{2^{log_{sin{frac{pi}{3}}}sqrt{2}}}	Смотреть видеоразбор

Про ЕГЭ: Чистые бланки ЕГЭ 2023 от официального сайта ФИПИ, правила заполнения бланков для 11 классов

5. Тригонометрические выражения

6. Нестандартные задачи (не входят в ЕГЭ)

Задание 1.

Найдите значение выражения $a^2-b^2=(sqrt{3})^2-(sqrt{13})^2=3-13=-10$

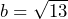
Ответ: -10.

Задание 2.

Найдите значение выражения $frac{(5sqrt{3})^2}{10}$ $frac{5^2 cdot (sqrt{3})^2}{10}=frac{25cdot3}{10}=frac{75}{10}=7,5$ $frac{5^2 cdot (sqrt{3})^2}{10}=frac{25cdot3}{10}=frac{75}{10}=7,5$

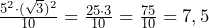
Ответ: 7,5.

Ничего сложного, если вы знаете формулы сокращенного умножения и свойства степеней.

А для того, чтобы найти значение выражения, в котором есть логарифмы, нужно знать свойства логарифмов.

Задание 3.

Найдите значение выражения $frac{log_{3}4}{log_{3}2} log_{2}0,5$

Здесь для нахождения значения выражения мы будем использовать следующие свойства логарифмов:

переход к новому основанию $log_{a}b=frac{log_{c}b}{log_{c}a}$ $log_{a}b log_{a}c=log_{a}{bc}$ $log_{a}b log_{a}c=log_{a}{bc}$ $frac{log_{3}4}{log_{3}2} log_{2}0,5=log_{2}4 log_{2}0,5=log_{2}{4cdot 0,5}=log_{2}2=1$

Ответ: 1.

Задание 4.

Найдите значение выражения $frac{(2^{frac{4}{7}}cdot 3^{frac{2}{3}})^{21}}{6^{12}}$ $(a^m cdot b^n)^k=a^{mk} cdot b^{nk}$ $(a^m cdot b^n)^k=a^{mk} cdot b^{nk}$

Преобразуем выражение в числителе дроби:

Разложим 6 на множители 2 и 3, получим:

Далее используем свойства степеней:

Сокращая числитель и знаменатель на $2^{12}$ $frac {2^{12}cdot 3^{14}}{2^{12} cdot 3^{12}}=3^{14-12}=3^2=9$ $frac {2^{12}cdot 3^{14}}{2^{12} cdot 3^{12}}=3^{14-12}=3^2=9$

Ответ: 9.

Задание 5

Найдите значение выражения: $frac {81^{2,6}}{9^{3,7}}$ $frac{(3^4)^{2,6}}{(3^2)^{3,7}}$ $frac{(3^4)^{2,6}}{(3^2)^{3,7}}$ $frac{(3^4)^{2,6}}{(3^2)^{3,7}}=frac{3^{4cdot 2,6}}{3^{2cdot 3,7}}=frac{3^{10,4}}{3^{7,4}}=3^{10,4-7,4}=3^3=27$

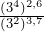
Ответ: 27.

Задание 6

Найдите значение выражения $log_{8}144-log_{8}2,25$ $log_{a}b-log_{a}c=log_{a}{frac{b}{c}}$ $log_{a}b-log_{a}c=log_{a}{frac{b}{c}}$ $log_{8}144-log_{8}2,25=log_{8}{frac{144}{2,25}}=log_{8}{64}=2$

Ответ: 2.

Задание 7

Найдите значение выражения $log_{4}40-log_{4}2,5$

Действуем также, как и в предыдущем задании, используя свойство разности логарифмов:

Ответ: 2.

Задание 8

Найдите

Для того, чтобы найти значение данного выражения нам понадобятся две тригонометрические формулы:

Основное тригонометрическое тождество: $cos^{2} {alpha} sin^{2} {alpha}=1$ .
Косинус двойного аргумента: $cos{2alpha}=cos^{2} {alpha}-sin^{2} {alpha}$ .

Итак, по формуле (2) распишем наше выражение в следующем виде: $28cos{2alpha}=28(cos^{2} {alpha}-sin^{2} {alpha})$ $sin^{2} {alpha}=1-cos^{2} {alpha}$ $sin^{2} {alpha}=1-cos^{2} {alpha}$

Тогда наше выражение примет вид:

Подставляем значение косинуса, получим:

Ответ: -0,56.

Задание 9

Найдите значение выражения $3sqrt{2}cos ^2 {frac{13 pi}{8}}-3sqrt{2}sin ^2 {frac{13 pi}{8}}$ $3sqrt{2}(cos ^2 {frac{13 pi}{8}}-sin ^2 {frac{13 pi}{8}})$ $cos{2alpha}=cos^{2} {alpha}-sin^{2} {alpha}$ $cos{2alpha}=cos^{2} {alpha}-sin^{2} {alpha}$ $cos {pi/4}=frac{sqrt{2}}{2}$ $cos {frac{13pi}{4}}$ $cos {frac{13pi}{4}}$ $frac{pi}{4}}$ $cos {frac{13pi}{4}}=cos{(3pi frac{pi}{4})}$ $cos {frac{13pi}{4}}=cos{(3pi frac{pi}{4})}$ $cos {frac{13pi}{4}}=cos{(3pi frac{pi}{4})}=-cos{frac{pi}{4}}=-frac{sqrt{2}}{2}$ $3sqrt{2} cos {frac{13 pi}{4}}$ $3sqrt{2} cos {frac{13 pi}{4}}$ $3sqrt{2} cos {frac{13 pi}{4}}=3sqrt{2} cdot(-frac{sqrt{2}}{2})=-3$

Ответ: -3.

Задания егэ профильного уровня по математике

Какие бывают задания с требованием найти значение выражения. Эти задания бывают разными и относящимися к разным темам. Например, выражения в задании 9 ЕГЭ по математике профильного уровня бывают:

степенные
логарифмические
тригонометрические
числовые
иррациональные (с корнями)
с переменными заданными величинами

Давайте рассмотрим общий принцип и необходимые теоретические сведения для решения каждого типа выражения.

Как решать 9 задание егэ 2022 математика профиль видео теория:

1)На рисунке изображён график функции вида f(x)= a3x b x c , где числа a, b и c — целые. Найдите a.

Про ЕГЭ: Методические рекомендации ЕГЭ 2021 по математике

2)На рисунке изображён график функции вида f(x)= 2ax b x c , где числа a, b и c — целые. Найдите a.

3)На рисунке изображён график функции вида f(x)= ax b x c , где числа a, b и c — целые. Найдите a.

4)На рисунке изображён график функции вида f(x)= a x b c, где числа a, b и c — целые. Найдите f(−22).

5)На рисунке изображён график функции вида f(x)= a x b c, где числа a, b и c — целые. Найдите решение уравнения f(x)=18.

6)На рисунке изображён график функции вида f(x)= 2ax b x c , где числа a, b и c — целые. Найдите a.

7)На рисунке изображён график функции вида f(x)= a x b c, где числа a, b и c — целые. Найдите f(15).

8)На рисунке изображён график функции вида f(x)= a x b c, где числа a, b и c — целые. Найдите x, при котором f(x)=21.

9)На рисунке изображён график функции вида f(x)=log5(ax b) c, где числа a, b, c  — целые. Найдите наибольшее значение функции g(x)=−x2 ax b.

10)На рисунке изображён график функции вида f(x)=log1.4(x−a) b, где числа a, b  — целые. Найдите ab.

11)На рисунке изображён график функции вида f(x)=2ax b, где числа a, b  — целые. Найдите сумму коэффициентов a b, если f(1)=10.

12)На рисунке изображён график функции вида f(x)=log2(ax b) 2, где числа a, b  — целые. Найдите сумму коэффициентов a b.

13)На рисунке изображён график функции вида f(x)=ln(a x) b, где числа a, b  — целые. Найдите сумму коэффициентов a b, если A(0;ln2e).

Первый вариант задания (демонстрационный вариант 2022)

[su_note note_color=”#defae6″]

Найдите sin2α , если cosα = 0,6 и π < α < 2π.

[/su_note]

Решу ЕГЭ 2022 задание №9 по математике 11 класс профильный уровень с ответами и решением для практики и подготовки к экзамену.

Пятый вариант задания (из ященко)

[su_note note_color=”#defae6″]
Найдите значение выражения

Про ЕГЭ: «Каково было количество сдавших экзамены в 2016 году и средние результаты ЕГЭ с 2010 по 2022 год по всем направлениям?»

.
[/su_note]

Решение:

1. Выражение содержит два корня.

2. Преобразовываем выражение и вычисляем его значение:

Ответ: 4.

Решу егэ 2022 тригонометрические функции 9 задание профиль математика с ответами:

Как формулируется новое задание 9 ЕГЭ 2022 по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Степенные выражения

Для того, чтобы найти значение выражения со степенями, вам понадобятся формулы для вычисления степеней. Приведем самые распространенные из них, на которые обычно дается задание нахождения значения выражения со степенями. Вы должны четко понимать, что если число находится в какой то степени, то оно не свободное, оно в отношении степени.

Например, вот здесь $frac{6^{5}}{2^{3}}$ $frac {3^{6,5}}{9^{2,25}}$ $frac {3^{6,5}}{9^{2,25}}$ $frac {3^{6,5}}{9^{2,25}}=frac{3^{6,5}}{(3^2)^{2,25}}=frac{3^{6,5}}{3^{4,5}}=3^{6,5-4,5}=3^2=9$

Здесь мы использовали свойство степени при делении степеней с одинаковыми основаниями. Приведем все необходимые для решения данных заданий свойства степеней:

Давайте рассмотрим еще несколько заданий.