Критерии оценивания егэ по математике
Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен
Критерии проверки и оценка решений задания 15 егэ–2022
Задание №15 – это неравенство – дробно-рациональное, логарифмическое или показательное.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением / включением граничных точек ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « 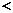 » вместо «
» вместо « 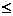 », или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов».
», или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов».
Задача 15 (демонстрационный вариант 2022 г).
Решите неравенство 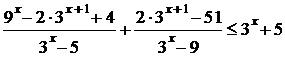 .
.
Решение.
Пусть 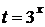 , тогда неравенство примет вид:
, тогда неравенство примет вид:
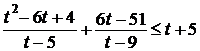 ;
; 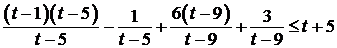 ;
;
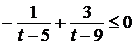 ;
;  ,
,
откуда 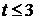 ;
; 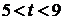 .
.
При 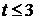 получим:
получим: 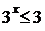 , откуда
, откуда 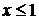 .
.
При 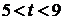 получим:
получим: 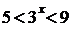 , откуда
, откуда 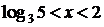 .
.
Решение исходного неравенства:
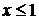 ;
; 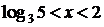 .
.
Ответ: 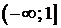 ;
; 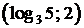 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точки 1, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Задача 1.
Решите неравенство  .
.
Решение.
Пусть 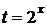 , тогда неравенство примет вид:
, тогда неравенство примет вид:
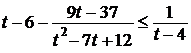 ;
; 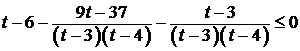 ;
;
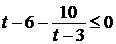 , где
, где 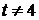 ;
; 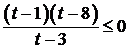 , где
, где 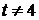 ,
,
откуда 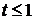 ;
; 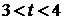 ;
; 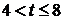 .
.
При 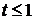 получим:
получим: 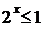 , откуда
, откуда 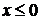 .
.
При 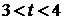 получим:
получим: 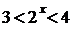 , откуда
, откуда 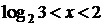 .
.
При 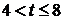 получим:
получим: 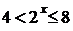 , откуда
, откуда 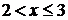 .
.
Решение исходного неравенства:
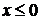 ;
; 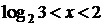 ;
; 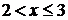 .
.
Ответ: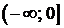 ;
; 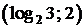 ;
; 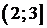 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точек 0 и/или 3, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Задача 2.
Решите неравенство 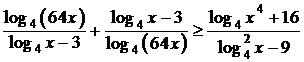 .
.
Решение.
Пусть 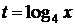 , тогда неравенство примет вид:
, тогда неравенство примет вид:
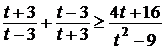 ;
; 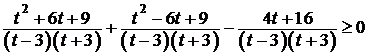 ;
;
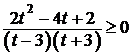 ;
; 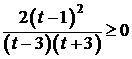 ,
,
откуда 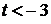 ;
; 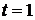 ;
; 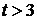 .
.
При 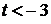 получим:
получим: 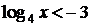 , откуда
, откуда 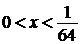 .
.
При 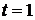 получим:
получим: 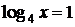 , откуда
, откуда 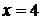 .
.
При 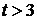 получим:
получим: 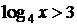 , откуда
, откуда 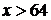 .
.
Решение исходного неравенства: 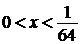 ;
; 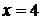 ;
; 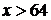 .
.
Ответ: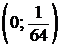 ; 4;
; 4;  .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением точки 4, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Примеры оценивания решений задания 15
Пример 1.
Решите неравенство  .
.
Ответ: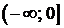 ;
; 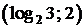 ;
; 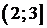 .
.

Комментарий.
Обоснованно получен верный ответ.
Оценка эксперта: 2 балла.
Пример 2.
Решите неравенство  .
.
Ответ: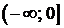 ;
; 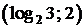 ;
; 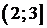 .
.

Комментарий.
В решение содержится запись «ОДЗ», которая может трактоваться по-разному.
Ответ получен неверный, но он отличается от верного только исключением точки 3.
Оценка эксперта: 1 балл.
Пример 3.
Решите неравенство  .
.
Ответ: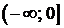 ;
; 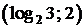 ;
; 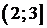 .
.
 .
.
Комментарий.
При решении неравенства допущена ошибка – допущен неравносильный переход. Это привело к неверному ответу.
Оценка эксперта. 0 баллов.
Пример 4.
Решите неравенство 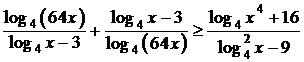 .
.
Ответ: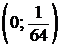 ; 4;
; 4;  .
.


Комментарий.
Обоснованно получен верный ответ.
Оценка эксперта. 2 балла.
Пример 5.
Решите неравенство 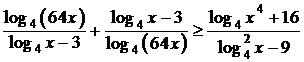 .
.
Ответ: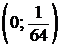 ; 4;
; 4;  .
.
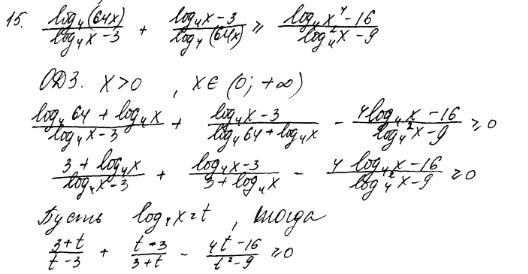
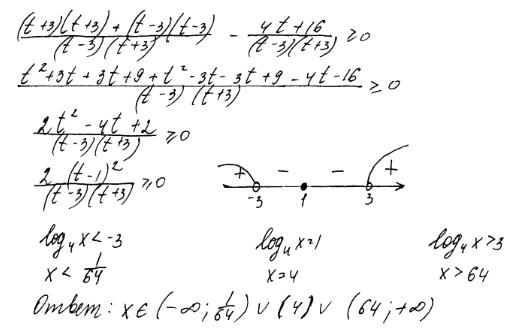
Комментарий.
При решении неравенства допущена ошибка при решении простейшего логарифмического неравенства. Ответ получен неверный. В решении содержится ошибочное утверждение, связанное с ОДЗ.
Оценка эксперта: 0 баллов.
Пример 6.
Решите неравенство 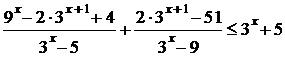 .
.
Ответ: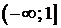 ;
; 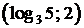 .
.

Комментарий.
Обоснованно получен верный ответ. Левая круглая скобка в ответе может быть прочитана как фигурная, но это не является основанием для того, чтобы считать ответ неверным.
Оценка эксперта. 2 балла.
Пример 7.
Решите неравенство 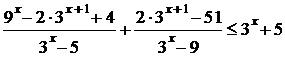 .
.
Ответ: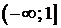 ;
; 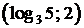 .
.

Комментарий.
В решении допущены ошибочные утверждения, присутствует неравносильный переход при решении неравенств, получен ответ (совпадающий с верным).
Оценка эксперта: 0 баллов.
Пример 8.
Решите неравенство 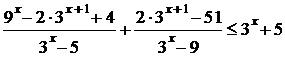 .
.
Ответ: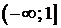 ;
; 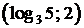 .
.

Комментарий.
Ответ неверный. При преобразовании числителя допущена вычислительная ошибка, но при этом имеется верная последовательность всех шагов решения.
Оценка эксперта: 1 балл.
§
Задание №16 – это планиметрическая задача. В пункте а теперь нужно доказать геометрический факт, в пункте б – найти (вычислить) геометрическую величину.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | 3 |
| Обоснованно получен верный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
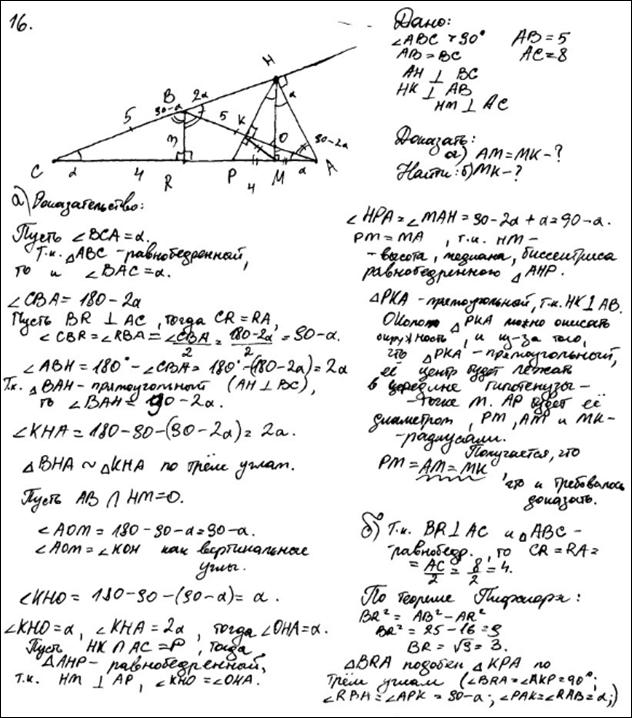
Задача 16 (демонстрационный вариант 2022 г).
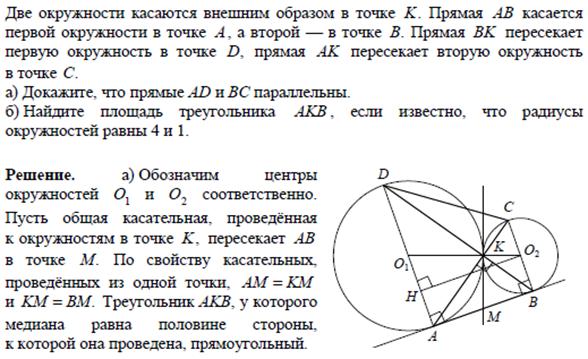

Задача 1.
В трапеции  боковая сторона
боковая сторона 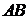 перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки 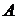 на сторону
на сторону 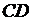 опустили перпендикуляр
опустили перпендикуляр 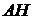 . На стороне
. На стороне 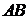 отмечена точка
отмечена точка 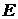 так, что прямые
так, что прямые 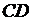 и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 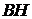 и
и 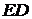 параллельны.
параллельны.
б) Найдите отношение 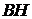 к
к 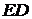 , если
, если  .
.
коэффициент подобия равен 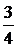 . Значит,
. Значит,
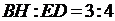 .
.
Ответ: б)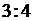 .
.
Задача 2.
В равнобедренном тупоугольном треугольнике 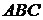 на продолжение боковой стороны
на продолжение боковой стороны 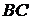 опущена высота
опущена высота 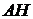 . Из точки
. Из точки 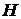 на сторону
на сторону 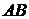 и основание
и основание 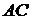 опущены перпендикуляры
опущены перпендикуляры 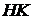 и
и 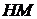 соответственно.
соответственно.
а) Докажите, что отрезки 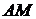 и
и 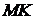 равны.
равны.
б) Найдите 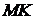 , если
, если 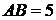 ,
, 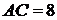 .
.
Решение.
б) В прямоугольных треугольниках  и
и  имеем:
имеем:
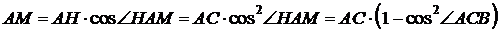 .
.
Поскольку 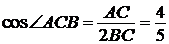 , получаем:
, получаем:
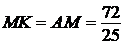 .
.
Ответ: б)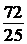 .
.
Примеры оценивания решений задания 16
Пример 1.
В трапеции  боковая сторона
боковая сторона 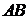 перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки 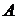 на сторону
на сторону 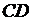 опустили перпендикуляр
опустили перпендикуляр 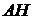 . На стороне
. На стороне 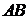 отмечена точка
отмечена точка 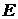 так, что прямые
так, что прямые 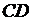 и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 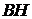 и
и 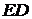 параллельны.
параллельны.
б) Найдите отношение 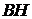 к
к 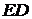 , если
, если 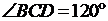 .
.
Ответ: б)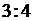 .
.
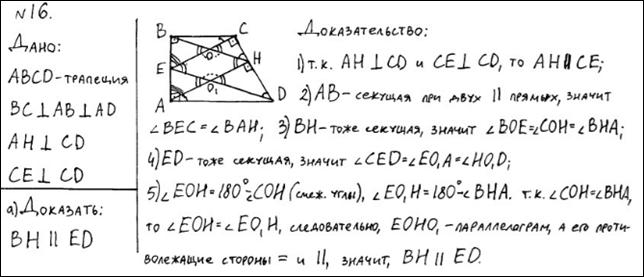
Комментарий.
Имеется попытка доказательства утверждения пункта а. Логическая ошибка содержится в записи 5) – при вычислении угла 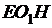 :
:  . Замена угла
. Замена угла  углом
углом 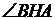 возможна только при условии параллельности прямых
возможна только при условии параллельности прямых 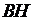 и
и 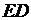 , а как раз это и требовалось доказать.
, а как раз это и требовалось доказать.
Оценка эксперта: 0 баллов.
Пример 2.
В трапеции 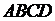 боковая сторона
боковая сторона 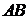 перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки 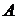 на сторону
на сторону 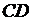 опустили перпендикуляр
опустили перпендикуляр 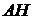 . На стороне
. На стороне 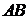 отмечена точка
отмечена точка 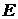 так, что прямые
так, что прямые 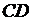 и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 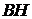 и
и 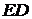 параллельны.
параллельны.
б) Найдите отношение 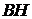 к
к 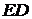 , если
, если 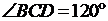 .
.
Ответ: б)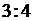 .
.

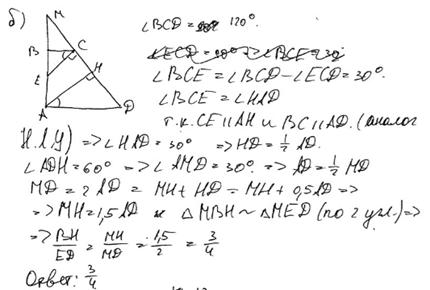
Комментарий.
В данном решении есть попытка доказательства утверждения пункта а. Логическая ошибка содержится в записи  – это возможно только при параллельности прямых
– это возможно только при параллельности прямых 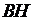 и
и 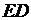 , а как раз это и требовалось доказать. Верный ответ в пункте б получен обоснованно с использованием недоказанного утверждения пункта а.
, а как раз это и требовалось доказать. Верный ответ в пункте б получен обоснованно с использованием недоказанного утверждения пункта а.
Оценка эксперта: 1 балл.
Пример 3.
В трапеции 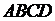 боковая сторона
боковая сторона 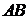 перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки 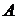 на сторону
на сторону 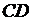 опустили перпендикуляр
опустили перпендикуляр 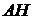 . На стороне
. На стороне 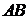 отмечена точка
отмечена точка 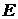 так, что прямые
так, что прямые 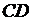 и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 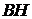 и
и 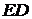 параллельны.
параллельны.
б) Найдите отношение 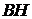 к
к 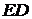 , если
, если 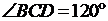 .
.
Ответ: б) .
.

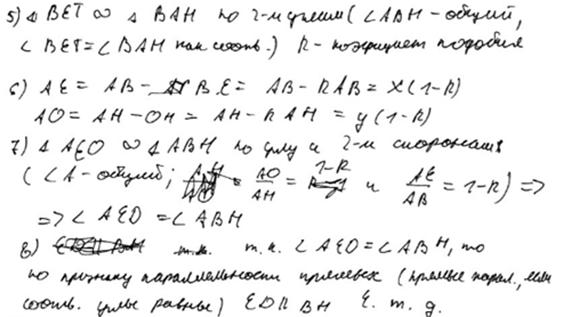
Комментарий.
Логическая ошибка: доказательство утверждения пункта а опирается на дополнительное условие из пункта б.
Оценка эксперта: 0 баллов.
Пример 4.
В равнобедренном тупоугольном треугольнике  на продолжение боковой стороны
на продолжение боковой стороны 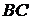 опущена высота
опущена высота 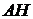 . Из точки
. Из точки 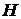 на сторону
на сторону 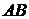 и основание
и основание 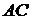 опущены перпендикуляры
опущены перпендикуляры 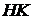 и
и 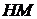 соответственно.
соответственно.
а) Докажите, что отрезки 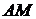 и
и 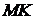 равны.
равны.
б) Найдите 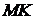 , если
, если 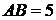 ,
, 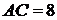 .
.
Ответ: б)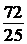 .
.

Комментарий.
Доказательство утверждения пункта а верно. Правда, следует отметить, что в доказательстве получено много верных утверждений, которые не нужны для доказательства равенства отрезков 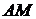 и
и 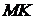 , кроме того некорректно формулируется признак подобия треугольников.
, кроме того некорректно формулируется признак подобия треугольников.
В решении пункта б допущена ошибка при вычислении длины отрезка 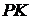 – вместо
– вместо 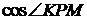 должно быть
должно быть 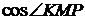 .
.
Оценка эксперта: 1 балл.
Пример 5.
В равнобедренном тупоугольном треугольнике 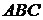 на продолжение боковой стороны
на продолжение боковой стороны 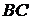 опущена высота
опущена высота 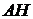 . Из точки
. Из точки 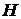 на сторону
на сторону 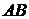 и основание
и основание 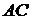 опущены перпендикуляры
опущены перпендикуляры 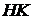 и
и 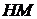 соответственно.
соответственно.
а) Докажите, что отрезки 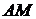 и
и 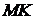 равны.
равны.
б) Найдите 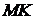 , если
, если 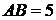 ,
, 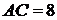 .
.
Ответ: б)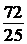 .
.
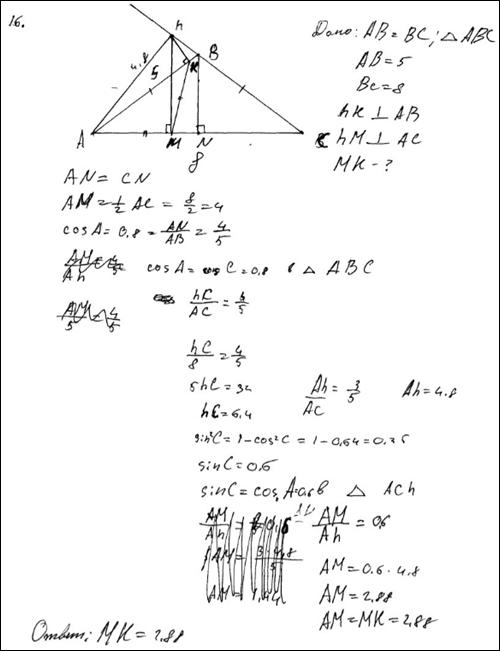
Комментарий.
Доказательство утверждения пункта а отсутствует. Решение пункта б выполнено верно с использованием недоказанного утверждения пункта а.
Оценка эксперта: 1 балл.
Пример 6.
В равнобедренном тупоугольном треугольнике  на продолжение боковой стороны
на продолжение боковой стороны  опущена высота
опущена высота 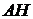 . Из точки
. Из точки 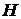 на сторону
на сторону 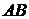 и основание
и основание 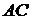 опущены перпендикуляры
опущены перпендикуляры 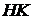 и
и 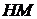 соответственно.
соответственно.
а) Докажите, что отрезки 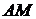 и
и 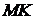 равны.
равны.
б) Найдите 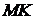 , если
, если 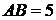 ,
, 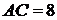 .
.
Ответ: б)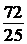 .
.
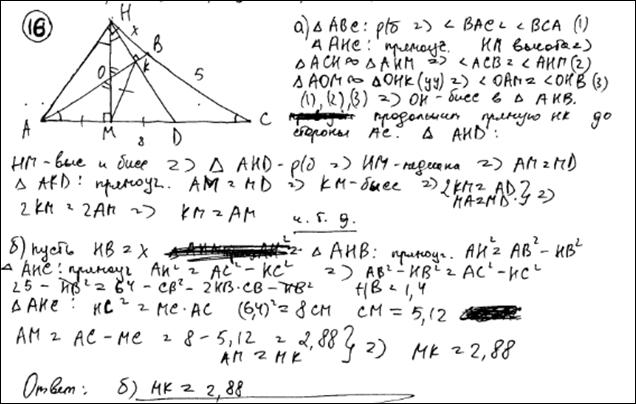
Комментарий.
В доказательстве утверждения пункта а есть некорректное утверждение – « 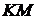 – биссектриса», при этом тут же записаны утверждения, соответствующие медиане прямоугольного треугольника.
– биссектриса», при этом тут же записаны утверждения, соответствующие медиане прямоугольного треугольника.
Решение пункта б выполнено верно.
Оценка эксперта: 3 балла.
§
Задание №17 – это текстовая задача с экономическим содержанием.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 3 |
| Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: — неверный ответ из-за вычислительной ошибки; — верный ответ, но решение недостаточно обосновано | 2 |
| Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Несколько подробнее: 1 балл можно выставлять в тех случаях, когда сюжетное условие задачи верно сведено к решению математической (арифметической, алгебраической, функциональной, геометрической) задачи. Именно к решению, а не к отдельному равенству, набору уравнений, уравнению, задающему функцию и т.п. Грубо говоря, предъявленный текст должен включать направление, «продолжаемое» до верного решения. Оценка в 2 балла, разумеется, включает в себя условие выставления 1 балла, но существенно ближе к верному решению задачи.
Здесь предполагается завершенное, практически полное решение соответствующей математической задачи. Типичные допустимые погрешности здесь – вычислительные ошибки (при наличии всех шагов решения) или недостаточно полные обоснования.
Отметим, что термин «математическая модель», быть может, излишне высокопарен для сравнительно простых задач экономического содержания, предлагаемых на ЕГЭ. Однако, по нашему мнению, он наиболее лаконичен, общеупотребим и достаточно ясен для того, чтобы пытаться отыскать ему адекватную замену. Следует подчеркнуть, что один и тот же сюжет может быть успешно сведен к различным математическим моделям и доведён до верного ответа. По этой причине в критериях проверки нигде нет жесткого упоминания о какой-либо конкретной (арифметической, алгебраической, геометрической, функциональной) модели.
Вообще, способов верного решения заданий этого типа никак не меньше, чем для привычных текстовых задач. Возможен и стиль, приближенный к высшей математике, и наивный подход, напоминающий арифметический способ решения текстовых задач, и метод использующий специфические для математической экономики понятия (целевая функция, симплекс-метод и т.п.).
Задача 17 (демонстрационный вариант 2022 г).

Задача 1.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на  процентов по сравнению с концом предыдущего месяца, где
процентов по сравнению с концом предыдущего месяца, где  — целое число;
— целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение 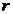 , при котором общая сумма выплат будет больше 1,2 млн рублей.
, при котором общая сумма выплат будет больше 1,2 млн рублей.
Решение.
По условию, долг перед банком (в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:
1; 0,9; 0,8; 0,7; 0,6; 0,5; 0.
Пусть 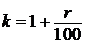 , тогда долг на 1-е число каждого месяца равен:
, тогда долг на 1-е число каждого месяца равен:
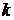 ;
; 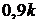 ;
;  ;
; 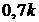 ;
; 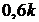 ;
; 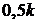 .
.
Следовательно, выплаты со 2-го по 14-е число каждого месяца составляют:
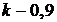 ;
; 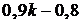 ;
; 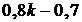 ;
; 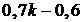 ;
; 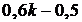 ;
; 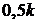 .
.
Общая сумма выплат составляет:
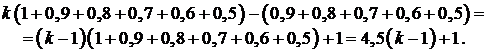
По условию, общая сумма выплат будет больше 1,2 млн рублей, значит,
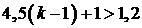 ;
; 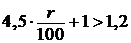 ;
; 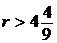 .
.
Наименьшее целое решение этого неравенства — число 5. Значит, искомое число процентов — 5.
Ответ: 5.
Задача 2.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на 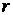 % по сравнению с концом предыдущего года;
% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите 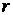 .
.
Решение.
Пусть сумма кредита составляет 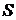 рублей, а ежегодные выплаты
рублей, а ежегодные выплаты 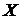 рублей,
рублей, 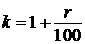 . По условию, долг перед банком (в рублях) по состоянию на июль должен уменьшаться следующим образом:
. По условию, долг перед банком (в рублях) по состоянию на июль должен уменьшаться следующим образом:
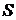 ,
, 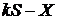 ,
, 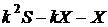 ,
, 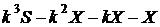 ,
,  .
.
Таким образом, если долг будет выплачен двумя равными платежами 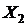 , то
, то
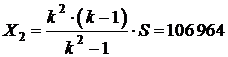 .
.
Если долг будет выплачен четырьмя равными платежами 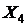 , то
, то
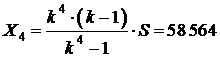 .
.
Таким образом, 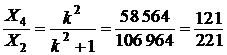 , откуда
, откуда 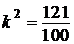 ;
; 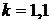 . Значит,
. Значит, 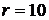 .
.
Ответ: 10.
§
Пример 1.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на 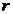 процентов по сравнению с концом предыдущего месяца, где
процентов по сравнению с концом предыдущего месяца, где 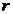 — целое число;
— целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение 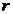 , при котором общая сумма выплат будет больше 1,2 млн рублей.
, при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.

Комментарий.
Модель построена неверно. Если подставить вместо  число 3 в таблицу, то сумма долга уже на 1 число второго месяца должна составить 4 млн рублей, кроме того, еще и неравенство решено неверно.
число 3 в таблицу, то сумма долга уже на 1 число второго месяца должна составить 4 млн рублей, кроме того, еще и неравенство решено неверно.
Оценка эксперта: 0 баллов.
Пример 2.
15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на  процентов по сравнению с концом предыдущего месяца, где
процентов по сравнению с концом предыдущего месяца, где 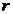 — целое число;
— целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение 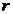 , при котором общая сумма выплат будет больше 1,2 млн рублей.
, при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.

Комментарий.
Модель построена верно. Усложняет проверку отсутствие вычислений. В таблице все результаты вычислений по формулам, записанным справа, верные. Логика решения верна.
Оценка эксперта: 3 балла.
Пример 3.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на 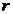 процентов по сравнению с концом предыдущего месяца, где
процентов по сравнению с концом предыдущего месяца, где 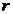 — целое число;
— целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение 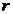 , при котором общая сумма выплат будет больше 1,2 млн рублей.
, при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.

Комментарий.
Почти правильное решение, содержащее ошибки (вычислительного характера). Две ошибки: 1)  , а не
, а не 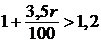 ; 2)
; 2) 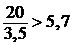 , т.е. должно быть
, т.е. должно быть 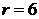 – не позволяют выставить 2 балла.
– не позволяют выставить 2 балла.
Оценка эксперта: 1 балл.
Пример 4.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на 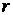 % по сравнению с концом предыдущего года;
% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите 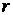 .
.
Ответ: 10.
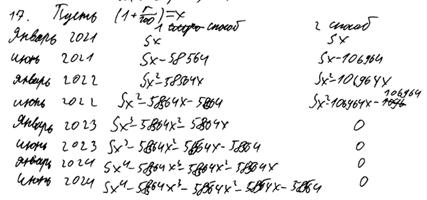

Комментарий.
Обоснованно получен верный ответ.
Оценка эксперта: 3 балла.
Пример 5.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на 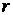 % по сравнению с концом предыдущего года;
% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите 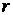 .
.
Ответ: 10.

Комментарий.
В решении без объяснений записаны уравнения. Переход от системы к уравнению относительно k не объяснен. Числовой ответ явно не получен: не извлечен корень из числа 14641. Таким образом, решение недостаточно обоснованное.
Оценка эксперта: 2 балла.
Пример 6.
15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на 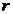 процентов по сравнению с концом предыдущего месяца, где
процентов по сравнению с концом предыдущего месяца, где 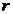 — целое число;
— целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму
в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0 |
Найдите наименьшее значение 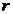 , при котором общая сумма выплат будет больше 1,2 млн рублей.
, при котором общая сумма выплат будет больше 1,2 млн рублей.
Ответ: 5.

Комментарий.
В решении без объяснений записано неравенство. Неравенство явно не решено. Таким образом, решение недостаточно обоснованное.
Оценка эксперта: 2 балла.
§
Задание №18 – это уравнение, неравенство или их системы с параметром.
Задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространенными из них являются:
– чисто алгебраический способ решения;
– способ решения, основанный на построении и исследовании геометрической модели данной задачи;
– функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.
Зачастую (но далеко не всегда) графический метод более ясно ведёт к цели. Кроме того, в конкретном тексте решения вполне могут встречаться элементы каждого из трех перечисленных способов.
Задача 18 (демонстрационный вариант 2022 г).


Задача 1
Найдите все значения 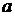 , при каждом из которых уравнение
, при каждом из которых уравнение
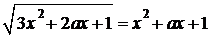 имеет ровно три различных корня.
имеет ровно три различных корня.
Решение.
Исходное уравнение равносильно уравнению 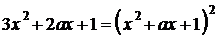
при условии 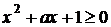 .
.
Решим уравнение 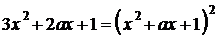 :
:
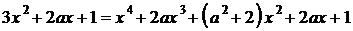 ;
;
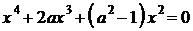 ;
; 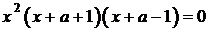 ,
,
откуда 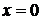 ,
,  или
или 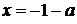 .
.
Исходное уравнение имеет три корня, когда эти числа различны
и для каждого из них выполнено условие 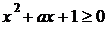 .
.
Рассмотрим условия совпадения корней. При 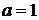 имеем
имеем 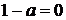 .
.
При 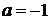 имеем
имеем 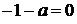 . При остальных значениях
. При остальных значениях 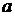 числа 0,
числа 0, 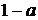 ,
, 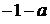 различны.
различны.
При 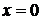 получаем:
получаем: 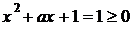 при всех значениях
при всех значениях 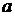 .
.
При  получаем:
получаем:
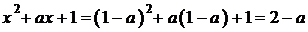 .
.
Это выражение неотрицательно при 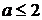 .
.
При 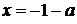 получаем:
получаем:
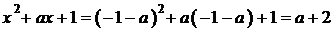 .
.
Это выражение неотрицательно при 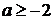 .
.
Таким образом, исходное уравнение имеет ровно три различных корня при
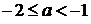 ;
; 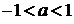 ;
; 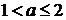 .
.
Ответ: 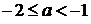 ;
; 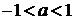 ;
; 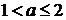 .
.
Задача 2.
Найдите все значения 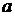 , при каждом из которых система уравнений
, при каждом из которых система уравнений
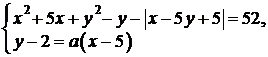
имеет ровно два решения.
Решение.
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим два случая:
1) Если 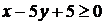 , то получаем уравнение
, то получаем уравнение
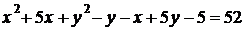 ;
;
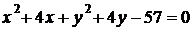 ;
;
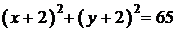 .
.
Полученное уравнение задаёт окружность с центром в точке 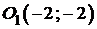
и радиусом 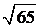 .
.
2) Если 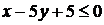 , то получаем уравнение
, то получаем уравнение
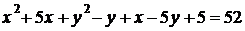 ;
; 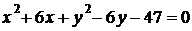 ;
; 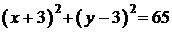 .
.
Полученное уравнение задаёт окружность с центром в точке 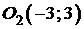
и радиусом 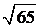 .
.
Полученные окружности пересекаются в двух точках 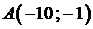 и
и 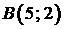 , лежащих на прямой
, лежащих на прямой 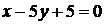 , поэтому в первом случае получаем дугу
, поэтому в первом случае получаем дугу 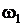 с концами в точках
с концами в точках 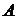 и
и 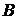 , во втором — дугу
, во втором — дугу  с концами в тех же точках (см. рис.).
с концами в тех же точках (см. рис.).
Рассмотрим второе уравнение системы. Оно задаёт прямую 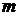 , которая проходит через точку
, которая проходит через точку 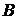 и угловой коэффициент которой равен
и угловой коэффициент которой равен 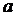 .
.
При 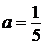 прямая
прямая 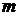 проходит через точки
проходит через точки 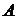 и
и 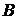 , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
При 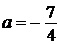 прямая
прямая  перпендикулярна прямой
перпендикулярна прямой  , угловой коэффициент которой равен
, угловой коэффициент которой равен 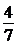 , значит, прямая
, значит, прямая 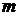 касается дуги
касается дуги 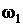 в точке
в точке 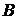 и пересекает дугу
и пересекает дугу 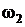 в двух точках (одна из которых — точка
в двух точках (одна из которых — точка 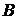 ), то есть исходная система имеет два решения.
), то есть исходная система имеет два решения.
При 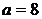 прямая
прямая 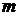 перпендикулярна прямой
перпендикулярна прямой 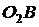 , угловой коэффициент которой равен
, угловой коэффициент которой равен 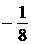 , значит, прямая
, значит, прямая 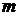 касается дуги
касается дуги 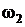 в точке
в точке 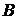
и пересекает дугу 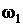 в двух точках (одна из которых — точка
в двух точках (одна из которых — точка 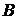 ), то есть исходная система имеет два решения.
), то есть исходная система имеет два решения.
При 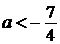 или
или 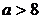 прямая
прямая 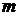 пересекает каждую из дуг
пересекает каждую из дуг 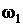 и
и 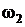 в точке
в точке 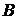
и ещё в одной точке, отличной от точки 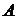 , то есть исходная система имеет три решения.
, то есть исходная система имеет три решения.
При 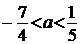 прямая
прямая 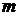 пересекает дугу
пересекает дугу 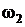 в двух точках (одна из которых — точка
в двух точках (одна из которых — точка 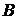 ) и не пересекает дугу
) и не пересекает дугу 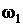 в точках, отличных от точки
в точках, отличных от точки 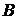 , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
При 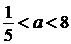 прямая
прямая 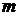 пересекает дугу
пересекает дугу 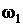 в двух точках (одна из которых — точка
в двух точках (одна из которых — точка 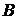 ) и не пересекает дугу
) и не пересекает дугу 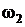 в точках, отличных от точки
в точках, отличных от точки 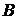 , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
Значит, исходная система имеет ровно два решения при 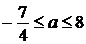 .
.
Ответ: 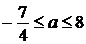 .
.
§
Пример 1.
Найдите все значения 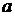 , при каждом из которых уравнение
, при каждом из которых уравнение
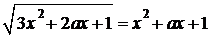 имеет ровно три различных корня.
имеет ровно три различных корня.
Ответ: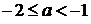 ;
; 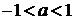 ;
; 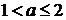 .
.

Комментарий.
Обоснованно получен верный ответ.
Оценка эксперта: 4 балла.
Пример 2.
Найдите все значения 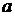 , при каждом из которых уравнение
, при каждом из которых уравнение
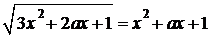 имеет ровно три различных корня.
имеет ровно три различных корня.
Ответ: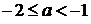 ;
; 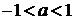 ;
; 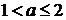 .
.


Комментарий.
Решение логично, все шаги присутствуют, но при решении неравенства в пункте 2) допущена ошибка вычислительного характера, что соответствует критерию на 2 балла.
Оценка эксперта: 2 балла.
Пример 3.
Найдите все значения 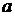 , при каждом из которых уравнение
, при каждом из которых уравнение
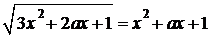 имеет ровно три различных корня.
имеет ровно три различных корня.
Ответ: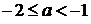 ;
; 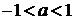 ;
; 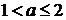 .
.
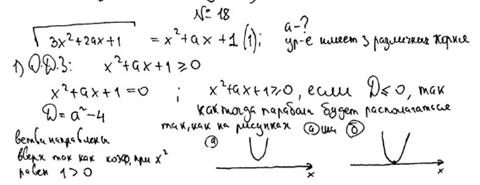
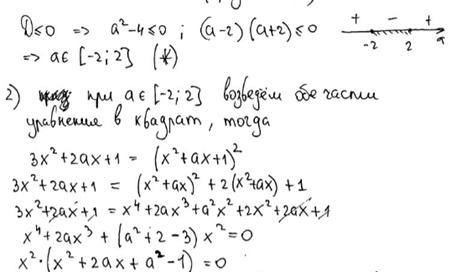
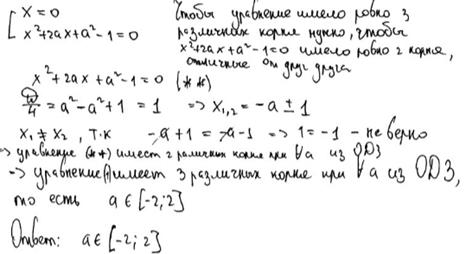
Комментарий.
Получены корни уравнения 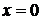 ,
,  ,
, 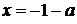 и задача сведена к исследованию полученных корней при условии
и задача сведена к исследованию полученных корней при условии 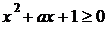 (есть только указание).
(есть только указание).
Оценка эксперта: 1 балл.
Пример 4.
Найдите все значения 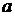 , при каждом из которых уравнение
, при каждом из которых уравнение
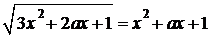 имеет ровно три различных корня.
имеет ровно три различных корня.
Ответ: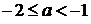 ;
; 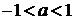 ;
; 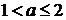 .
.


Комментарий.
В решении присутствуют все этапы. Решение соответствует критерию на 3 балла: с помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек 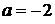 и/или
и/или 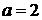 .
.
Оценка эксперта: 3 балла.
Пример 5.
Найдите все значения 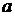 , при каждом из которых система уравнений
, при каждом из которых система уравнений
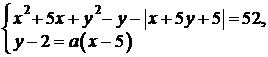
имеет ровно два решения.
Ответ: 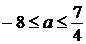 .
.
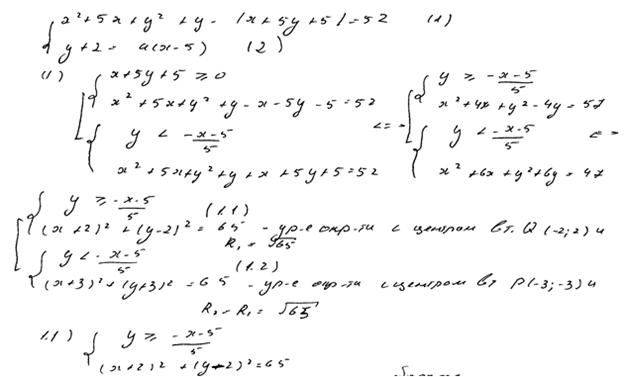
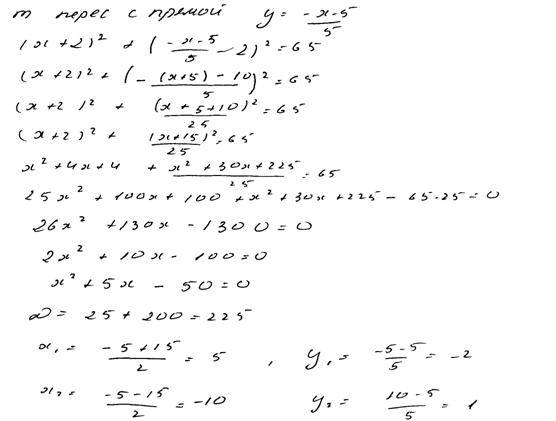
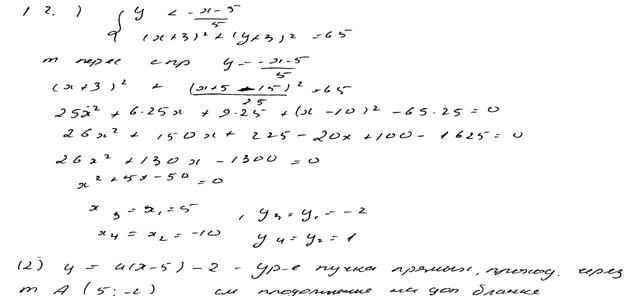
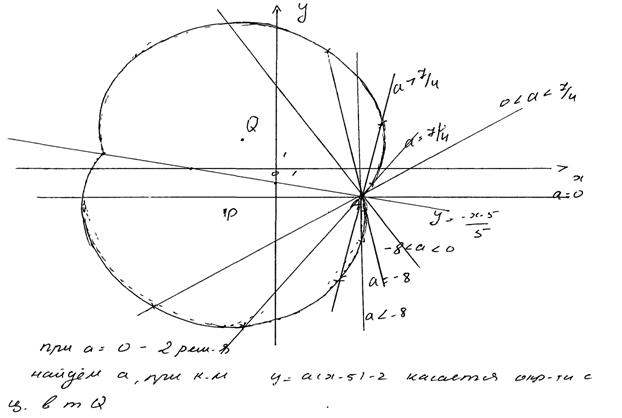
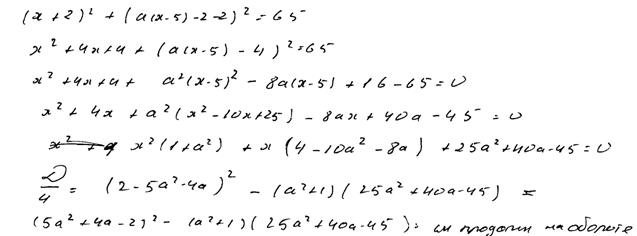
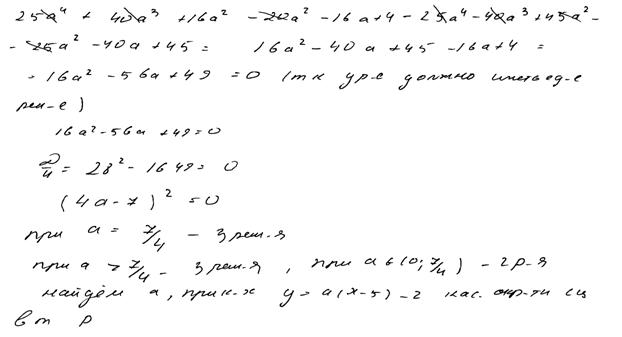

Комментарий.
Ход решения ясен, изложен более чем подробно. Ошибок нет, кроме недочета: концы промежутка не включены в ответ.
Оценка эксперта: 3 балла.
Пример 6.
Найдите все значения 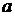 , при каждом из которых система уравнений
, при каждом из которых система уравнений
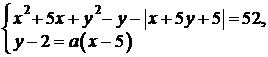
имеет ровно два решения.
Ответ: 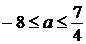 .
.
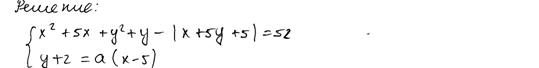
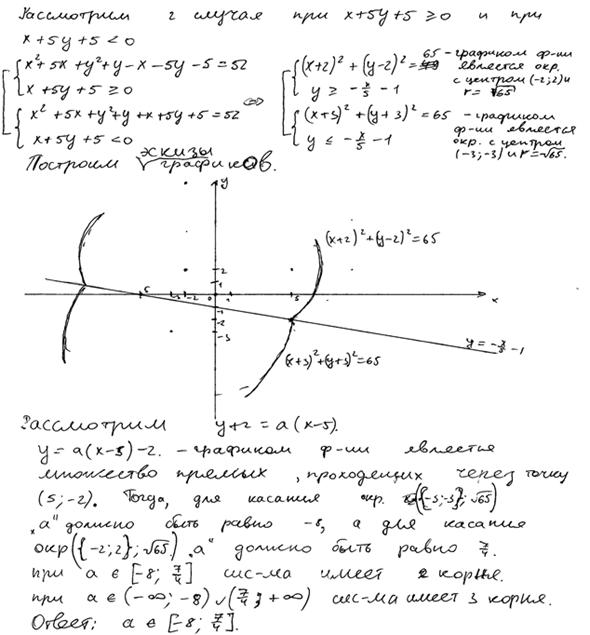
Комментарий.
Решение и ответ верные, хотя нет обоснования, почему для касания 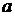 «
«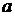 должно быть равно –8» или «…7/4».
должно быть равно –8» или «…7/4».
Оценка эксперта: 4 балла.
Критерии проверки и оценка решений заданий 19 ЕГЭ-2022
Содержательно задание №19 проверяет в первую очередь не уровень математической (школьной) образованности, а уровень математической культуры. Формирования культуры происходит на протяжении всех лет обучения (и не только в школе). Для решения этой задачи никаких фактов из теории чисел типа теоремы Вильсона, чисел Мерсенна, малой теоремы Ферма, теории сравнений и т.п. для решения этих заданий не требуется. Тот, кто эти факты знает, разумеется, может их использовать, но, подчёркиваем, при решении всегда можно обойтись и без них.
Условия задания №19 разбиты на пункты. По существу, задача разбита на ряд подзадач (частных случаев), последовательно решая которые можно в итоге справится с ситуацией в целом.
Задача 19 (демонстрационный вариант 2022 г).


Задача 1.
В последовательности 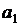 ,
, 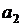 , …,
, …, 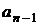 ,
, 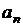 , состоящей из целых чисел,
, состоящей из целых чисел, 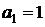 ,
, 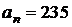 . Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
. Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Решение.
а) Например, последовательность 1, 2, 3, 0, 5, 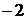 , 7,
, 7, 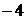 , …, 233,
, …, 233, 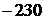 , 235
, 235
удовлетворяет условию задачи (чередуются суммы чисел 3 и 5).
б) Поскольку 3, 5 и 25 — нечётные числа, любые два соседних члена последовательности имеют разную чётность. На нечётных местах должны стоять нечётные числа, а на чётных — чётные. Число 235 нечётное, поэтому оно не может стоять на чётном месте. Значит, последовательность не может состоять из 1000 членов.
в) Рассмотрим три члена последовательности: 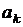 ,
, 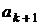 ,
, 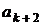
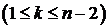 .
.
Поскольку 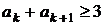 ,
, 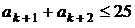 , получаем:
, получаем: 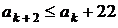 .
.
В предыдущем пункте было показано, что последовательность должна состоять из нечётного числа членов. Пусть 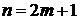 , тогда
, тогда
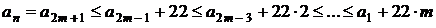 ;
; 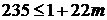 ,
,
откуда 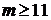 . Значит, последовательность состоит не менее чем из 23 чисел.
. Значит, последовательность состоит не менее чем из 23 чисел.
Приведём пример последовательности, удовлетворяющей условию задачи, состоящей из 23 членов: 1, 2, 23, 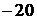 , 45,
, 45, 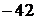 , 67,
, 67, 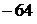 , 89,
, 89, 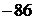 , 111,
, 111, 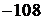 ,
, 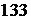 ,
, 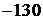 , 155,
, 155, 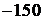 , 175,
, 175, 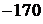 , 195,
, 195, 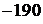 , 215,
, 215, 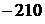 , 235.
, 235.
Ответ: а) например, 1, 2, 3, 0, 5, 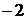 , 7,
, 7, 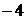 , …, 233,
, …, 233, 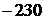 , 235; б) нет; в) 23.
, 235; б) нет; в) 23.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | 2 |
| Верно получен один из следующих результатов: — пример в п. а; — обоснованное решение п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Задача 2.
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны
и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 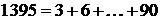 , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Решение.
а) Если на доске записано 29 зелёных чисел: 3, 6, …, 87 — и одно красное
число 21, то их сумма меньше 1395.
б) Пусть на доске ровно одно красное число. Тогда зелёных чисел 29,
а их сумма не меньше, чем сумма 29 наименьших чисел, делящихся на 3:
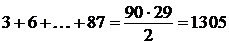 .
.
Это противоречит тому, что сумма написанных чисел равна 1067.
в) Пусть на доске написано 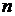 красных чисел и
красных чисел и 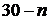 зелёных чисел. Тогда сумма красных чисел не меньше
зелёных чисел. Тогда сумма красных чисел не меньше 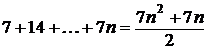 ,
,
а сумма зелёных чисел не меньше
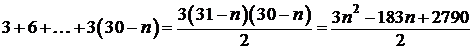 .
.
Таким образом, 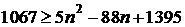 ;
; 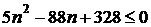 ,
,
откуда, учитывая, что 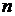 — целое, получаем
— целое, получаем 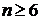 .
.
Приведём пример 6 красных чисел и 24 зелёных чисел, сумма которых
равна 1067: 7, 14, 21, 28, 35, 56, 3, 6, …, 66, 69, 78.
Ответ: а) да; б) нет; в) 6.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | 4 |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | 3 |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | 2 |
| Верно получен один из следующих результатов: — обоснованное решение пункта а; — обоснованное решение пункта б; — искомая оценка в пункте в; — пример в пункте в, обеспечивающий точность предыдущей оценки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
§
Пример 1.
В последовательности 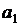 ,
, 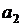 , …,
, …, 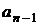 ,
, 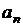 , состоящей из целых чисел,
, состоящей из целых чисел, 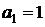 ,
, 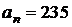 . Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
. Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Ответ: а) например, 1, 2, 3, 0, 5, 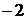 , 7,
, 7, 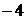 , …, 233,
, …, 233, 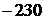 , 235; б) нет; в) 23.
, 235; б) нет; в) 23.

Комментарий.
В пункте а допущена ошибка – сумма первых двух чисел равна –25. При ответе на вопрос пункта б участник экзамена верно показал, что случай 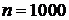 невозможен.
невозможен.
Оценка эксперта: 1 балл.
Пример 2.
В последовательности 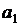 ,
, 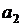 , …,
, …, 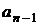 ,
, 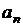 , состоящей из целых чисел,
, состоящей из целых чисел, 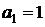 ,
, 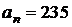 . Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
. Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Ответ: а) например, 1, 2, 3, 0, 5, 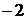 , 7,
, 7, 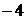 , …, 233,
, …, 233, 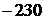 , 235; б) нет; в) 23.
, 235; б) нет; в) 23.

Комментарий.
В пункте а верно приведен пример. Решение пункта б неверно.
Оценка эксперта: 1 балл.
Пример 3.
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны
и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 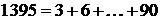 , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Ответ: а) да; б) нет; в) 6.


Комментарий.
Приведено верное решение пункта а. Приведено верное решение пункта б.
Решение в пункте в не завершено.
Оценка эксперта: 2 балла.
Пример 4.
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны
и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 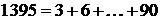 , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Ответ: а) да; б) нет; в) 6.


Комментарий.
Обоснованно получены верные ответы во всех пунктах.
Оценка эксперта: 4 балла.
Пример 5.
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны
и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 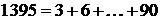 , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Ответ: а) да; б) нет; в) 6.

Комментарий.
Обоснованно получен ответ в пунктах а и б. В решении пункта в есть логическая ошибка: не доказано, что красных чисел не может быть меньше 5. Взяв пять красных, нужно взять 25 зеленых чисел, а не 26. Кроме того, сумма чисел найдена неверно.
Оценка эксперта: 2 балла.
Указания по оцениваю развернутых ответов участников ЕГЭ
для эксперта, проверяющего развёрнутые ответы
на задания 13–19 по МАТЕМАТИКЕ
(документ предоставляется эксперту при проведении оценивания экзаменационных работ вместе с критериями оценивания)
Эксперт, проверяющий задания с развернутым ответом, располагает следующими материалами:
1) тексты заданий;
2) возможный вариант решения каждой задачи 13–19;
3) критерии оценивания заданий 13–19.
При проверке заданий с развернутым ответом эксперт имеет возможность пользоваться непрограммируемым калькулятором.
В критериях оценивания выполнения заданий с развернутым ответом КИМ ЕГЭ по математике для каждого задания приводится один возможный вариант решения. Однако предлагаемый разработчиками КИМ способ (метод) решения не является эталонным. Он лишь помогает эксперту в решении соответствующего задания.
Выполнение заданий оценивается в соответствии с критериями оценивания ответов на задания с развернутым ответом. Принципом построения системы оценивания является оценка продвижений участника экзамена в решении задачи в виде достижения формализованных в критериях промежуточных результатов. Максимальный балл выставляется только при наличии в тексте решения обоснованно полученного правильного ответа. Наличие в тексте решения недостатка в обосновании ответа или вычислительной ошибки не позволяет выставить за решение задания в соответствии с критериями максимальный балл. В случае, когда решение не подпадает ни под один из критериев положительных баллов (не достигнут ни один промежуточный математический результат), выполнение задания оценивается 0 баллов.
При использовании обобщенной схемы оценивания ответов на каждое из заданий 13-19рекомендуется обращать внимание на следующие моменты:
ü Перед проведением проверки выполнения каждого из заданий необходимо изучить критерии его оценивания в материалах для эксперта, обратив внимание на детализацию и конкретизацию обобщенной схемы оценивания применительно к конкретному заданию.
ü Решение участника экзамена может иметь логику, отличную от логики решения, данного в критериях (альтернативное решение). В этом случае эксперт оценивает допустимость решения конкретной задачи тем способом, который выбрал участник экзамена. Если ход решения допустим, то эксперт оценивает обоснованность этого решения на основании той совокупности свойств (признаков), формул или утверждений, которые соответствуют выбранному способу решения.
ü Участник экзамена может использовать без доказательства математические факты и формулы, содержащиеся в учебниках, входящих в Федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования (далее – Федеральный перечень).
ü Если экзаменуемый использует в решении без доказательства формулы и факты, которые не представлены в учебниках, входящих в Федеральный перечень, то такое решение классифицируется как недостаточно обоснованное.
ü Если математические преобразования, представленные в решении, не отражают основных необходимых логических шагов, то решение не может оцениваться максимальным баллом.
ü Если при решении геометрической задачи использует рисунок, то ошибки в соотношении длин отрезков на рисунке, не влекут за собой снижения баллов за решение геометрической задачи, если на рисунке верно отображена геометрическая конфигурация и верно обозначены точки, описанные в решении.
ü При проверке правильности решения необходимо проверять корректность промежуточных шагов решения, в том числе числовых выкладок (при необходимости, с помощью калькулятора). Наличие ошибок в промежуточных выкладках, даже не повлиявших на итоговый ответ, означает наличие математически некорректного перехода в решении задачи, что не позволяет оценить решение задачи максимальным баллом.
ü Если участник экзамена решает задачу с другими числовыми данными, то такое решение задачи оценивается в 0 баллов, даже если он решают содержательно более сложную задачу.
ü При проверке решения каждого из заданий 13–19 необходимо вычленить в решении три элемента:
— логика (последовательность и закономерность) решения,
— обоснованность решения,
— числовой ответ.
Количество логических шагов в решении и перечень условий и закономерностей зависит от выбранного способа решения. Это необходимо учитывать при применении критериев оценивания выполнения задания с развернутым ответом.
В процессе проверки необходимо придерживаться следующих общих правил:
ü При работе эксперт выставляет свои оценки в протокол проверки развернутых ответов.
ü Выставление баллов в протокол проверки развернутых ответов рекомендуется проводить по работам: все задания первой проверяемой работы, все задания второй проверяемой работы и т.д. Это позволяет обнаружить ошибки, допущенные экзаменуемым в нумерации задач, а также обнаружить непронумерованную, или пронумерованную неверно, или случайно пропущенную экспертом задачу. Ошибочное указание участником экзамена номера задачи, которую он выполняет, не может служить основанием для снижения оценки за фактически выполненное задание.
ü Результаты оценивания переносятся в протокол проверки развернутых ответов, при этом баллы по каждому заданию переносятся в колонку, название которой соответствует номеру задания (см. Рисунок 1):
— баллы по заданию 13 переносятся в колонку 13протокола;
— баллы по заданию 14 переносятся в колонку 14протокола;
— баллы по заданию 15 переносятся в колонку 15протокола;
— баллы по заданию 16 переносятся в колонку 16протокола;
— баллы по заданию 17 переносятся в колонку 17протокола;
— баллы по заданию 18 переносятся в колонку 18протокола;
— баллы по заданию 19 переносятся в колонку 19протокола.
ü Баллы выставляются в протокол проверки гелевой черной ручкой.
ü Внесение изменений в протокол проверки крайне нежелательно. Все исправления вносятся только поверх неверных записей. Использование замазок и затирок с целью исправления записей категорически недопустимо!
Рисунок 1. Протокол проверки развернутых ответов 2022 года. Образец.

Внимание!При выставлении баллов за выполнение задания в Протокол проверки развернутых ответов следует иметь в виду, что если ответ отсутствует (нет никаких записей, свидетельствующих о том, что экзаменуемый приступал к выполнению задания), то в протокол проставляется «Х», а не «0». Если в работе записан только номер задания без попыток ее решения, то в протокол выставляется «0».
Пример 6.
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны
и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 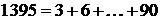 , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Ответ: а) да; б) нет; в) 6.

Комментарий.
Обоснованно получен ответ в пунктах а и б. В пункте в неверное обоснование, поскольку не доказано, что набор с минимальным количеством красных чисел получается заменой максимальных чисел из набора 3, 6, …, 90 на минимально возможные различные красные числа. Кроме того, разница между пятью самыми большими зелеными числами и пятью самыми маленькими красными числами составляет 315.
Оценка эксперта: 2 балла.
Подать документы
Заполните заявку на обучение или приходите в приемную комиссию, которая находится по адресу: м. Текстильщики, Москва, ул. Артюхиной, д. 6, корп. 1 (каб. 112, часы работы 10:00—18:00 по будням и 10:00—15:00 в субботу)
Для поступления требуется заполнить ряд заявлений и предоставить следующие документы*:
- паспорт (страницы с фотографией и регистрацией)
- оригинал документа установленного образца о предыдущем образовании либо его копия, заверенная нотариально, либо его копия с предъявлением оригинала для заверения копии приемной комиссией
- 2 фотографии 3х4 (матовые, цветные или черно-белые)
*Документы, полученные в образовательных учреждениях иностранных государств, должны пройти процедуру признания, если требуется.
Решу егэ
Результаты участников профильного экзамена 2021 г. близки к результатам 2022 г. и несколько выше результатов 2020 г., что может быть связано с совершенствованием дистанционной формы обучения во многих регионах, где в 2020 г. могли наблюдаться значительные трудности с обеспечением доступа обучающихся и учителей к дистанционным учебным платформам.
Более подробные аналитические и методические материалы ЕГЭ 2021 года доступны по ссылке.
ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ЕГЭ ПО МАТЕМАТИКЕ 2022 ГОДА
читать полностью: спецификация.
Обозначение уровня сложности задания: Б — базовый, П — повышенный, В — высокий.
Проверяемые элементы содержания и виды деятельности | Уровень сложности задания | Максимальный балл за выполнение задания | Примерное время выполнения задания (мин.) | |
| Задание 1. Уметь решать уравнения и неравенства | Б | 1 | 5 | 2 |
| Задание 2. Уметь строить и исследовать простейшие математические модели | Б | 1 | 5 | 2 |
| Задание 3. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | Б | 1 | 5 | 3 |
| Задание 4. Уметь выполнять вычисления и преобразования | Б | 1 | 5 | 3 |
| Задание 5. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | Б | 1 | 10 | 3 |
| Задание 6. Уметь выполнять действия с функциями | Б | 1 | 10 | 4 |
| Задание 7. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни | П | 1 | 15 | 6 |
| Задание 8. Уметь строить и исследовать простейшие математические модели | П | 1 | 15 | 7 |
| Задание 9. Уметь выполнять действия с функциями | П | 1 | 15 | 8 |
| Задание 10. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни | П | 1 | 15 | 8 |
| Задание 11. Уметь выполнять действия с функциями | П | 1 | 15 | 9 |
| Задание 12. Уметь решать уравнения и неравенства | П | 2 | 20 | 10 |
| Задание 13. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | П | 3 | 40 | 20 |
| Задание 14. Уметь решать уравнения и неравенства | П | 2 | 30 | 15 |
| Задание 15. Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни | П | 2 | 30 | 25 |
| Задание 16. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | П | 3 | 35 | |
| Задание 17. Уметь решать уравнения и неравенства | В | 4 | 35 | |
| Задание 18. Уметь строить и исследовать простейшие математические модели | В | 4 | 40 | |
ОФИЦИАЛЬНАЯ ШКАЛА 2022 ГОДА
Соответствие между минимальными первичными баллами и минимальными тестовыми баллами 2022 года. Распоряжение о внесении изменений в приложение № 2 к распоряжению Федеральной службы по надзору в сфере образования и науки. Перейти.
ПОРОГОВЫЕ БАЛЛЫ
Для получения аттестата: 27 тестовых (5 первичных) баллов. См. распоряжение Рособрнадзора.
Для поступления в вузы, подведомственные Министерству науки и высшей школы: 39 тестовых баллов. См. приказ Миннауки.
Для поступления в вузы, подведомственные Министерству просвещения: 39 тестовых баллов. См. приказ Минпроса.
ЭКЗАМЕНАЦИОННЫЕ БЛАНКИ
Правила заполнения бланков государственной итоговой аттестации. Скачать бланки в высоком качестве можно по ссылке.
 ЧТО МОЖНО ВЗЯТЬ С СОБОЙ НА ЭКЗАМЕН
ЧТО МОЖНО ВЗЯТЬ С СОБОЙ НА ЭКЗАМЕН
На экзамене по математике разрешается пользоваться линейкой, которая не содержит справочную информацию, для построения чертежей и рисунков. Источник.
Задания базовой части ЕГЭ по математике взяты из открытого банка экзаменационных заданий (http://mathege.ru) и представляют собой модельные задачи, на основе которых путем изменения конкретных числовых данных составляются реальные экзаменационные работы ЕГЭ. Задания повышенного и высокого уровня сложности были специально составлены для портала «РЕШУ ЕГЭ» или предлагались в официальных сборниках для подготовки к экзамену.
Авторы задач для подготовки к ЕГЭ:
И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров,
Р. К. Гордин,
А. В. Малышев,
С. В. Панферов, М. А. Посицельская, С. Е. Посицельский,
М. Я. Пратусевич,
С. Е. Рукшин,
А. В. Семенов, А. Л. Семенов, И. Н. Сергеев,
К. М. Столбов,
В. А. Смирнов,
С. А. Шестаков, Д. Э. Шноль, И. В. Ященко;
материалы сайта http://ege.yandex.ru.
Наверх








