ЕГЭ Демо 2017 Профильный уровень

ЕГЭ Демо 2017 Профильный уровень ЕГЭ
На чтение 7 мин. Просмотров 35 Опубликовано
Содержание
  1. Демонстрационные варианты (демоверсии) егэ по математике
  2. Ответы
  3. Решение демоварианта кимов для егэ 2022 года по математике (профильный уровень)
  4. Условия задач

Демонстрационные варианты (демоверсии) егэ по математике

Демонстрационные варианты ЕГЭ по математике для 11 класса за 2002-2009 годы включали в себя три раздела: А (задачи с выбором ответа из нескольких предложенных), В (задачи с кратким ответом) и С (задания, для выполнения которых требовалось привести полное решение задачи).

В 2022 году из демонстрационного варианта ЕГЭ по математике были исключены задачи с выбором ответа, ранее составлявшие раздел А. Таким образом, демонстрационный вариант ЕГЭ стал состоять уже только из двух разделов В и С.

Демонстрационный вариант ЕГЭ 2022 года почти полностью совпадал с демонстрационным вариантом ЕГЭ 2022 года: были изменены лишь задания C1 и C5.

В 2022 году в демонстрационном варианте ЕГЭ по математике тематических изменений по сравнению с предыдущим годом не было: задачи В3, В9, В14, С2 и С4 были заменены на другие задачи той же тематики. Кроме того, было добавлено задание базового уровня сложности с кратким ответом, проверяющее практические навыки применения математики в повседневной жизни и изменен порядок заданий.

В 2022 году в порядке проведения ЕГЭ по математике произошли серьезные изменения: было решено проводить два отдельных экзамена – базового уровня и профильного уровня.

В связи с этим в 2022 году было представлено 2 демонстрационных варианта: новая модель демонстрационного варианта для ЕГЭ базового уровня и модернизированная модель демонстрационного варианта 2022 года для проведения ЕГЭ профильного уровня.

Демонстрационный вариант для ЕГЭ базового уровня содержал только задания базового уровня сложности с кратким ответом (20 заданий). В демонстрационном варианте было представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы на каждую позицию было предложено только одно задание.

Демонстрационный вариант профильного экзамена 2022 года разработан на основе демонстрационного варианта ЕГЭ по математике 2022 года со следующими изменениями:

В демонстрационном варианте ЕГЭ по математике базового уровня 2022 года изменений не было .

Про ЕГЭ:  Элективный курс по литературе при подготовке к ЕГЭ по Авторской программе элективной компьютерной подготовки «Подготовка к ЕГЭ по информатике и ИКТ» (10-11 классы)

В демонстрационном варианте ЕГЭ по математике профильного уровня 2022 года произошли следующие изменения:

В демонстрационных вариантах ЕГЭ по математике 2022 — 2021 годов как базового уровня, так и профильного уровня, по сравнению с демонстрационными вариантами ЕГЭ по математике 2022 года изменений не было.

В демонстрационном варианте ЕГЭ по математике 2022 года базового уровня по сравнению с демонстрационным вариантом ЕГЭ по математике 2021 года базового уровня произошли следующие изменения:

В демонстрационном варианте ЕГЭ по математике 2022 года профильного уровня по сравнению с демонстрационным вариантом ЕГЭ по математике 2021 года профильного уровня произошли следующие изменения:

  • Удалены задания 1 и 2, проверяющие умение использовать приобретённые знания и умения в практической и повседневной жизни, и задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.
  • Добавлены задание 9, проверяющее умение выполнять действия с функциями, и задание 10, проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
  • Внесены изменения в систему оценивания: максимальный балл за выполнение задания повышенного уровня 13, проверяющего умение выполнять действия с геометрическими фигурами, координатами и векторами, стал равен 3; максимальный балл за выполнение задания повышенного уровня 15, проверяющего умение использовать приобретённые знания и умения в практической деятельности и повседневной жизни, стал равен 2.
  • Количество заданий уменьшилось с 19 до 18, максимальный балл за выполнение всей работы стал равным 31.

Ответы

  1. 8
  2. 4
  3. 6
  4. 0,08
  5. 9
  6. 64
  7. 4
  8. 4
  9. -0,96
  10. 751
  11. 5
  12. -5
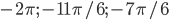
  13. а) pi n, nin Z, (-1)^kpi/6 pi k, kin Z б) -2pi; -11pi/6; -7pi/6
  14. б) arcsinsqrt{3/8}
  15. 3,2
  16. 7
  17. а) 44; б) отрицательных; в) 17.

Решение демоварианта кимов для егэ 2022 года по математике (профильный уровень)

При ознакомлении с демонстрационным вариантом контрольных измерительных материалов ЕГЭ 2022 г. следует иметь в виду, что задания, включённые в него, не отражают всех вопросов содержания, которые будут проверяться с помощью вариантов КИМ в 2022 г. Полный перечень вопросов, которые могут контролироваться на едином государственном экзамене 2022 г., приведён в кодификаторе элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена 2022 г. по математике.
Назначение демонстрационного варианта заключается в том, чтобы дать возможность любому участнику ЕГЭ и широкой общественности составить представление о структуре будущих КИМ, количестве заданий, об их форме и уровне сложности. Приведённые критерии оценки выполнения заданий с развёрнутым ответом, включённые в этот вариант, дают представление о требованиях к полноте и правильности записи развёрнутого ответа.
Эти сведения позволят выпускникам выработать стратегию подготовки к ЕГЭ.

Про ЕГЭ:  Решение демоварианта КИМов для ЕГЭ 2017 года по МАТЕМАТИКЕ (профильный уровень)

ЗАДАНИЯ

РЕШЕНИЯ

Условия задач

Часть 1

  1. Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
  2. На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 г. По горизонтали указаны номера месяцев; по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией.  Сколько месяцев средняя температура была больше 18 градусов Цельсия? ЕГЭ Демо 2017 Профильный уровень
  3. На клетчатой бумаге с размером клетки 1 см х 1 см изображён треугольник. Найдите его площадь. Ответ дайте в см2. ЕГЭ Демо 2017 Профильный уровень
  4. В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
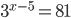
  5. Найдите корень уравнения 3^{x-5}=81
  6. Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32o. Найдите угол BOC . Ответ дайте в градусах.
  7. На рисунке изображён график дифференцируемой функции 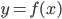y=f(x). На оси абсцисс отмечены девять точек: 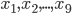x_1,x_2,...,x_9.  Найдите все отмеченные точки, в которых производная функции 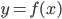y=f(x) отрицательна. В ответе укажите количество этих точек. ЕГЭ Демо 2017 Профильный уровень
  8. В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ выразите в см.
    Часть 2
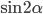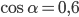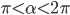  9. Найдите sin2alpha, если cosalpha = 0,6 и pi<alpha<2pi.
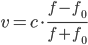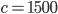  10. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением v = ccdotdisplaystylefrac{f-f_0}{f f_0}, где c=1500 м/c  — скорость звука в воде; 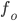f_o — частота испускаемого сигнала (в МГц); 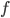f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
  11. Весной катер идёт против течения реки в 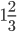1displaystylefrac{2}{3} раза медленнее, чем по течению.Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 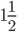1displaystylefrac{1}{2} раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
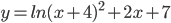
  12. Найдите точку максимума функции y=ln(x 4)^2 2x 7
  13. а) Решите уравнение cos2x=1-cos(frac{pi}{2}-x).
    б) Найдите все корни этого уравнения, принадлежащие промежутку [-frac{5pi}{2};-pi).
  14. Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N — середины рёбер AA1 и A1C 1 соответственно.
    а) Докажите, что прямые BM и MN перпендикулярны.
    б) Найдите угол между плоскостями BMN и ABB1.
  15. Решите неравенство displaystylefrac{9^x-2cdot3^{x 1} 4}{3^x-5} frac{2cdot3^{x 1}-51}{3^x-9}le3^x 5
  16. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
    а) Докажите, что прямые AD и BC параллельны.
    б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
  17. 15-го января планируется взять кредит в банке на шесть месяцев
    в размере 1 млн рублей. Условия его возврата таковы:
    — 1-го числа каждого месяца долг увеличивается на r процентов
    по сравнению с концом предыдущего месяца, где r — целое число;
    — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
    — 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей ЕГЭ Демо 2017 Профильный уровень  Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
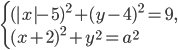  18. Найдите все положительные значения a, при каждом из которых система left{begin{array}{l l} (|x|-5)^2 (y-4)^2=9,\ (x 2)^2 y^2=a^2end{array}right. имеет единственное решение.
  19. На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно -3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно -8.
    а) Сколько чисел написано на доске?
    б) Каких чисел написано больше: положительных или отрицательных?
    в) Какое наибольшее количество положительных чисел может быть среди них?
Про ЕГЭ:  Задание №17 ЕГЭ по математике профильного уровня ⋆ СПАДИЛО
2017 ЕГЭ Базовый Государственный демо демоверсия единый Кодификатор математика ОГЭ профильный уровень скачать Спецификация утвержден Экзамен
Оцените статью
ЕГЭ Live
© 2024 ЕГЭ Live