- Тренировочные варианты «школково». основная волна. реальные варианты егэ 2022
- Егэ 2022. математика. профильный. практикум. экзаменационные тесты. к новой официальной версии егэ
- Тренировочный вариант егэ 2022 по математике профильного уровня с ответами и критериями. пробный егэ по математике, январь 2022
Тренировочные варианты «школково». основная волна. реальные варианты егэ 2022
а) Пусть (O_1) и (O_2) центры большей и меньшей окружностей соответственно. Так как (O_1M) и (O_2M) перпендикулярны касательной, проходящей через точку (M), то точки (O_1), (O_2) и (M) лежат на одной прямой. Пусть (M’) – точка пересечения этой прямой с большей окружностью, отличная от (M).
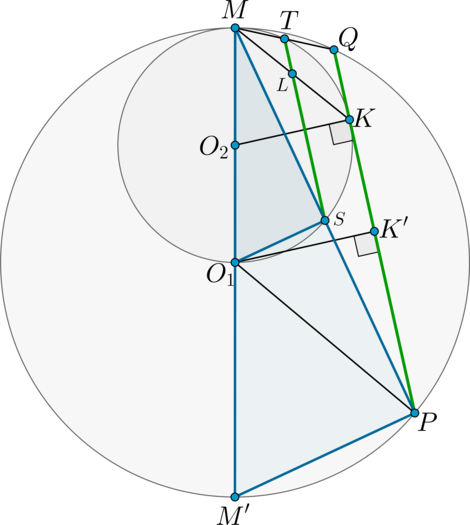
Докажем, что хорды данных окружностей, лежащие на одной прямой, проходящей через точку (M), относятся как их диаметры. Рассмотрим доказательство на примере хорд (MS) и (MP).
Рассмотрим треугольники (MM’P) и (MO_1S). Эти треугольники прямоугольные, так как (MO_1) – диаметр меньшей окружности (описанной около треугольника (MO_1S)), а (MM’) – диаметр большей окружности (описанной около треугольника (MM’P)). При этом острый угол (O_1MS) у них общий, следовательно, эти треугольники подобны.
Из подобия получаем требуемое: [dfrac{MS}{MP} = dfrac{MO_1}{MM’}]
Для других хорд, лежащих на прямой, проходящей через точку (M), утверждение доказывается аналогично.
Из доказанного следует, что [dfrac{MS}{MP} = dfrac{MT}{MQ},.]
Рассмотрим треугольники (MST) и (MPQ): (angle SMQ) – общий, (dfrac{MS}{MP} = dfrac{MT}{MQ}), следовательно, эти треугольники подобны, откуда (angle MST = angle MPQ), следовательно, (STparallel PQ).
б) Опустим перпендикуляры (O_1K’) и (O_2K) на (PQ).
По теореме Пифагора [K’O_1^2 = O_1P^2 — K’P^2]
Так как (O_1P = O_1Q), то (O_1K’) – медиана в треугольнике (PO_1Q), следовательно, (K’P = 3), тогда (K’O_1 = sqrt{25 — 9} = 4).
Так как (MO_1) – радиус большей окружности и диаметр меньшей, то радиус меньшей окружности равен (0,5cdot 5 = 2,5)
Рассмотрим прямоугольную трапецию (O_2O_1K’K).
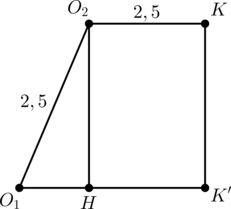
Пусть (O_2H) перпендикуляр к (O_1K’), тогда (O_1H = O_1K’ — O_2K =
4-2,5=1,5), следовательно, по теореме Пифагора (2 = O_2H = KK’). Тогда [PK = PK’ K’K=3 2=5,qquad KQ = PK’-K’K=3-2=1.]
Так как хорды данных окружностей, лежащие на одной прямой, проходящей через точку (M), относятся как их диаметры, то (ST) – средняя линия в треугольнике (MPQ), тогда (SL) – средняя линия в треугольнике (MPK) и (LT) – средняя линия в треугольнике (MKQ), следовательно, [SL = 0,5PK=2,5,qquad LT = 0,5KQ=0,5,.]
По теореме о произведении отрезков хорд [MLcdot LK = SLcdot LT = 1,25=dfrac54,,] откуда, с учётом равенства (ML = LK), получим [ML =
dfrac{sqrt{5}}{2},.]
Ответ:
б) (dfrac{sqrt{5}}{2})
Егэ 2022. математика. профильный. практикум. экзаменационные тесты. к новой официальной версии егэ
Практикум ЕГЭ по математике предназначен как для работы в классе, так и для самостоятельного контроля знаний.
Предлагаемое пособие содержит тренировочные варианты тестовых заданий Единого государственного экзамена (ЕГЭ) по математике (профильный уровень), составленные с учетом всех особенностей и требований ЕГЭ, ориентированные на тех учащихся, для которых математика является обязательным предметом при поступлении в выбранный вуз.
Практикум предназначен учителям и методистам, использующим тесты для подготовки учащихся к Единому государственному экзамену, он также может быть использован учащимися для самоподготовки и самоконтроля.
Приказом № 729 Министерства образования и науки Российской Федерации учебные пособия издательства «Экзамен» допущены к использованию в общеобразовательных организациях.
СОДЕРЖАНИЕ
ВАРИАНТ 1
Часть 1
Часть 2
ВАРИАНТ 2
Часть 1
Часть 2
ВАРИАНТ 3
Часть 1
Часть 2
ВАРИАНТ 4
Часть 1
Часть 2
ВАРИАНТ 5
Часть 1
Часть 2
ВАРИАНТ 6
Часть 1
Часть 2
ВАРИАНТ 7
Часть 1
Часть 2
ВАРИАНТ 8
Часть 1
Часть 2
ВАРИАНТ 9
Часть 1
Часть 2
ВАРИАНТ 10
Часть 1
Часть 2
ОТВЕТЫ
РЕШЕНИЕ ВАРИАНТА 5
Часть 1
Часть 2
ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮ РАБОТЫ
Работа состоит из 15 заданий повышенного и высокого уровня сложности и предназначена для проверки освоения математики на профильном уровне. Работа предназначена для учащихся, нацеленных на применение математики в дальнейшей профессиональной деятельности.
Работа состоит из двух частей. Первая часть включает 8 заданий с кратким ответом 1-8. Ответом к каждому из них является целое число или конечная десятичная дробь.
Часть 2 содержит 7 заданий (9—15) по материалу курса математики средней школы. Каждое из этих заданий требует записи полного решения и ответа.
При выполнении заданий Вы можете пользоваться черновиком. На выполнение работы даётся 3 часа 55 минут (235 минут). Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Тренировочный вариант егэ 2022 по математике профильного уровня с ответами и критериями. пробный егэ по математике, январь 2022
- 12.02.2022
4 варианта пробного ЕГЭ по математике 2022 года с ответами и критериями для проверки части С (15-21 задания).
Уровень заданий — профильный.
В конце представлены критерии для самостоятельной проверки заданий с развёрнутым ответом.
Обсудить сложные задания или спорные задачи вы можете ниже, в комментариях.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.









