В9. гиперболы | подготовка к егэ по математике
Задача 1. На рисунке изображён график функции Найдите
Найдите
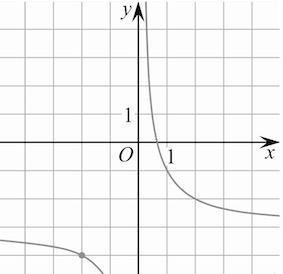
Решение: показать
Задача 2. На рисунке изображён график функции вида где числа
где числа
и
— целые. Найдите значение
— целые. Найдите значение
, при котором

Решение: показать
Задача 3. На рисунке изображён график функции вида где
где
– целые числа. Найдите

Решение: показать
Задача 4. На рисунке изображён график функции Найдите
Найдите

Решение: показать
Задача 5. На рисунке изображены графики функций и
и
и которые пересекаются в точках
и
и
. Найдите ординату точки

Решение: показать

Вы можете пройти тест “Гиперболы”
Решу егэ
Ясно, что
иначе
а тогда графиком функции была бы прямая. Излом графика находится в точке
а потому, раскрывая модуль, получаем:
Горизонтальная прямая, содержащая правую ветвь графика, задается уравнением Тангенс угла наклона левой части графика к оси абсцисс равен −4, а продолжение левой части графика пересекает ось ординат в точке −7. Поэтому
С другой стороны, в любом из случаев раскрытия модуля получаем линейную функцию, угловой коэффициент которой или
а свободный член
или
Очевидно, что
значит, большему значению углового коэффициента соответствует
а меньшему —
Аналогично большему значению свободного члена соответствует
а меньшему соответствует
Итак,
Сравнивая (⁎) и (⁎⁎), получаем систему уравнений: Сложим первые два и последние два уравнения системы, получим
Тогда
откуда для уравнения
получаем
Ответ: −3.








