- Тренировочные варианты «школково». основная волна. реальные варианты егэ 2022
- Апробация ким егэ, базовый уровень (октябрь 2022)
- Демоверсия егэ 2022
- Демонстрационный вариант огэ 2022
- Диагностическая работа по математике апрель 2022
- Диагностическая работа по математике (5 марта 2022)
- Диагностическая работа по математике (февраль 2022)
- Диагностическая работа по математике (январь 2022)
- Досрочный егэ по математике (26 марта 2022)
- Досрочный егэ по математике (резервный день)
- Кимы с досрочного егэ-2022
- Огэ от 27 мая 2022 г.
- Пробный егэ 2022 по математике: профильный уровень с ответами
- Реальный егэ по математике (4 июня 2022)
- Решу егэ
- Тренировочная работа по математике апрель 2022
Тренировочные варианты «школково». основная волна. реальные варианты егэ 2022
а) Пусть (O_1) и (O_2) центры большей и меньшей окружностей соответственно. Так как (O_1M) и (O_2M) перпендикулярны касательной, проходящей через точку (M), то точки (O_1), (O_2) и (M) лежат на одной прямой. Пусть (M’) – точка пересечения этой прямой с большей окружностью, отличная от (M).
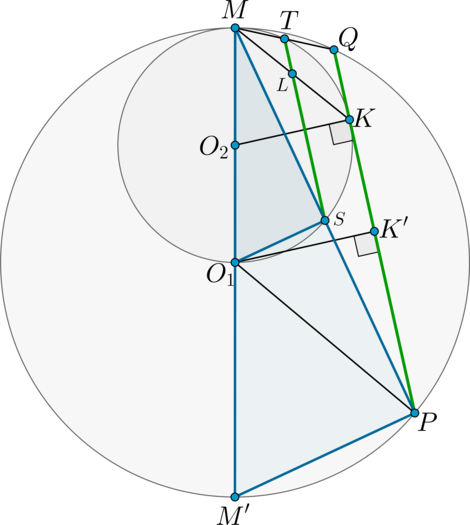
Докажем, что хорды данных окружностей, лежащие на одной прямой, проходящей через точку (M), относятся как их диаметры. Рассмотрим доказательство на примере хорд (MS) и (MP).
Рассмотрим треугольники (MM’P) и (MO_1S). Эти треугольники прямоугольные, так как (MO_1) – диаметр меньшей окружности (описанной около треугольника (MO_1S)), а (MM’) – диаметр большей окружности (описанной около треугольника (MM’P)). При этом острый угол (O_1MS) у них общий, следовательно, эти треугольники подобны.
Из подобия получаем требуемое: [dfrac{MS}{MP} = dfrac{MO_1}{MM’}]
Для других хорд, лежащих на прямой, проходящей через точку (M), утверждение доказывается аналогично.
Из доказанного следует, что [dfrac{MS}{MP} = dfrac{MT}{MQ},.]
Рассмотрим треугольники (MST) и (MPQ): (angle SMQ) – общий, (dfrac{MS}{MP} = dfrac{MT}{MQ}), следовательно, эти треугольники подобны, откуда (angle MST = angle MPQ), следовательно, (STparallel PQ).
б) Опустим перпендикуляры (O_1K’) и (O_2K) на (PQ).
По теореме Пифагора [K’O_1^2 = O_1P^2 — K’P^2]
Так как (O_1P = O_1Q), то (O_1K’) – медиана в треугольнике (PO_1Q), следовательно, (K’P = 3), тогда (K’O_1 = sqrt{25 — 9} = 4).
Так как (MO_1) – радиус большей окружности и диаметр меньшей, то радиус меньшей окружности равен (0,5cdot 5 = 2,5)
Рассмотрим прямоугольную трапецию (O_2O_1K’K).
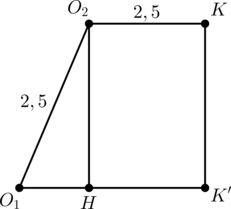
Пусть (O_2H) перпендикуляр к (O_1K’), тогда (O_1H = O_1K’ — O_2K =
4-2,5=1,5), следовательно, по теореме Пифагора (2 = O_2H = KK’). Тогда [PK = PK’ K’K=3 2=5,qquad KQ = PK’-K’K=3-2=1.]
Так как хорды данных окружностей, лежащие на одной прямой, проходящей через точку (M), относятся как их диаметры, то (ST) – средняя линия в треугольнике (MPQ), тогда (SL) – средняя линия в треугольнике (MPK) и (LT) – средняя линия в треугольнике (MKQ), следовательно, [SL = 0,5PK=2,5,qquad LT = 0,5KQ=0,5,.]
По теореме о произведении отрезков хорд [MLcdot LK = SLcdot LT = 1,25=dfrac54,,] откуда, с учётом равенства (ML = LK), получим [ML =
dfrac{sqrt{5}}{2},.]
Ответ:
б) (dfrac{sqrt{5}}{2})
Апробация ким егэ, базовый уровень (октябрь 2022)
1, 2, 3, 4, 5, 6, 7
Демоверсия егэ 2022
Демоверсия базового ЕГЭ по математике 2022
Демоверсия профильного ЕГЭ по математике 2022
Демонстрационный вариант огэ 2022
Демо версия ОГЭ 2022
Диагностическая работа по математике апрель 2022
профильный уровень, разбор на сайте 1-20, 15-21 (критерии)
базовый уровень
Диагностическая работа по математике (5 марта 2022)
профильный уровень
Диагностическая работа по математике (февраль 2022)
базовый уровень
Диагностическая работа по математике (январь 2022)
профильный уровень
базовый уровень
Досрочный егэ по математике (26 марта 2022)
профильный уровень (с критериями)
Досрочный егэ по математике (резервный день)
профильный уровень (задания 15-21)
Кимы с досрочного егэ-2022
→ Русский язык — 01.pdf
→ Математика (базовый уровень) — 22.pdf Ответы и решение заданий: dv-math-baza.rar
→ Математика (профильный уровень) — 02.pdf
→ Физика — 03.pdf
→ Химия — 04.pdfПодробный разбор заданий.
→ Информатика и икт — 05.pdfПодробный разбор заданий.
→ Биология — 06.pdf
→ История — 07.pdf
→ Обществознание — 12.pdf
→ География — 08.pdf
→ Английский язык — 09.pdf
→ Немецкий язык — 10.pdf
→ Французский язык — 11.pdf
→ Испанский язык — 13.pdf
→ Литература — 18.pdf
2 — тоже
3 — 4
4 — запертый
5 — удачным
6 — болеекрасива
7 — 52471
8 — утопический
9 — ненаглядныйзайти
10 — заманчивый
11 — значимый
12 — неясные
13 — совсемнаперекор
14 — 1234
15 — 23
16 — 12
17 — 1234
18 — 1
19 — 234
20 — 14
21 — 134
22 — сильногослабому
23 — 31
24 — 6375
2 — 9
3 — 210
4 — 0,6
5 — 0,16
6 — 4,5
7 — 3,5
8 — 4
9 — 28
10 — 5
11 — 7
12 — 86
13 — 60
14 — 29
2 — 4
3 — 3
4 — 46
5 — 3
6 — 2
7 — 1
8 — 3
9 — 236
10 — 4
11 — 2
12 — 125
13 — 1
14 — 4
15 — 1
16 — 246
17 — 4
18 — 2
19 — 1
20 — 145
21 — 246
22 — репродуктивная
23 — 3
24 — 26
25 — 12121
2 — 1
3 — 3
4 — 4
5 — 1
6 — 2
7 — 3
8 — 4
9 — 2
10 — 3
11 — 4
12 — 4
13 — 1
14 — 2
15 — 3
16 — 4
17 — 1
18 — 2
19 — 4
20 — 3
21 — 2
22 — 13524
23 — 236
24 — 5241
25 — 5
26 — дружина
27 — 542687
28 — 136
29 — четырнадцатый
30 — Коломна
31 — Мамай
32 — 256
33 — 35
34 — 3
2 — 4
3 — 3
4 — 4
5 — 1
6 — 1
7 — 3
8 — 1
9 — 3
10 — 2
11 — 4
12 — 2
13 — 2
14 — 3
15 — 1
16 — 1
17 — 2
18 — 3
19 — 1
20 — 4
21 — 3
22 — 4
23 — 4
24 — 1
25 — 4
26 — 2
27 — 6214
28 — 4436
29 — 2442
30 — 3122
31 — 5123
32 — 2155
33 — 346
34 — 234
35 — 156
2 — 4
3 — 1,5
4 — 5
5 — 100
6 — 22
7 — 12
8 — 4
9 — 3
10 — 100
11 — 13
12 — 12
13 — 2
14 — 1
15 — 3
16 — 0,6
17 — 23
18 — 13
19 — 1
20 — 3
21 — 20
22 — 23
23 — 2
24 — 34
25 — 0,1
2 — 1
3 — 4
4 — 1
5 — 2
6 — 1
7 — 3
8 — 3
9 — 4
10 — 2
11 — 2
12 — 1
13 — 4
14 — 2
15 — 3
16 — 4
17 — 4
18 — 3
19 — 2
20 — 2
21 — 3
22 — 2
23 — 2
24 — 1
25 — 4
26 — 126
27 — 356
28 — 236
29 — 12112
30 — 212121
31 — 221212
32 — 313123
33 — 415263
Для каждого часового пояса разрабатывались отдельные комплекты контрольных измерительных материалов, соответствующих ранее опубликованным на демоверсиям, спецификациям и кодификаторам КИМ ЕГЭ 2022 г.
Также рекомендуем посмотреть — КИМы с досрочного ЕГЭ-2022.
Огэ от 27 мая 2022 г.
ОГЭ по математике
Пробный егэ 2022 по математике: профильный уровень с ответами
- 02.08.2022
Напоминаем, что с 2022 года ЕГЭ по математике будет разделён на два уровня — профильный и базовый.
Предлагаем вашему вниманию первый пробный ЕГЭ 2022 по математике профильного уровня.
Вариант содержит полностью часть В и С. Ответы в конце файла, мы предлагаем вам свои ответы сверять и обсуждать решения в комментариях.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Реальный егэ по математике (4 июня 2022)
Образец варианта
Решу егэ
Ученики одной школы писали тест. Результатом каждого участника является целое неотрицательное число баллов. Ученик считается сдавшим тест, если он набрал не менее 83 баллов. Из-за того, что задания оказались слишком трудными, было принято решение всем участникам теста добавить по 5 баллов, благодаря чему количество сдавших тест увеличилось.
а) Могло ли оказаться так, что после этого средний балл учеников, не сдавших тест, понизился?
б) Могло ли оказаться так, что после этого средний балл учеников, сдавших тест, понизился, и средний балл учеников, не сдавших тест, тоже понизился?
в) Известно, что первоначально средний балл участников теста составил 90, средний балл учеников, сдавших тест, составил 100, а средний балл учеников, не сдавших тест, составил 75. После добавления баллов средний балл учеников, сдавших тест, стал равен 103, а не сдавших — 79. При каком наименьшем числе участников теста возможна такая ситуация?
Тренировочная работа по математике апрель 2022
профильный уровень








